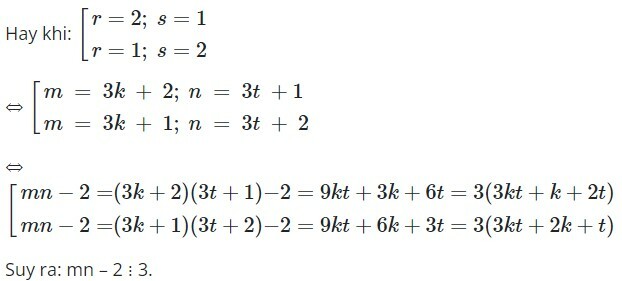Chứng minh rằng: (x^m + x^n + 1) chia hết cho x^2 + x + 1 khi và chỉ khi (mn – 2) chia hết cho 3

Câu 8: Chứng minh rằng: (x^m + xⁿ + 1) chia hết cho x² + x + 1 khi và chỉ khi (mn – 2) chia hết cho 3.

Trả lời

Đặt m = 3k + r với 0 ≤ r ≤ 2

n = 3t + s với 0 ≤ s ≤ 2

Ta có: x^m + xⁿ + 1

= x^3k+r + x^3t+s + 1

= x^3kx^r – x^r + x^3tx^s – x^s + x^r + x^s + 1

= x^r (x^3k – 1) + x^s (x^3t – 1) + x^r + x^s + 1

Ta thấy: (x^3k – 1) ⋮ (x² + x + 1) và (x^3t – 1) ⋮ (x² + x + 1)

Vậy để (x^m + xⁿ + 1) ⋮ x² + x + 1 thì (x^r + x^s + 1) ⋮ (x² + x + 1) với 0 ≤ r, s ≤ 2