Chứng minh hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Chứng minh hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Lời giải
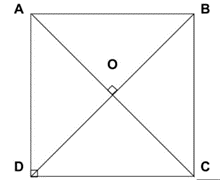
Hình chữ nhật ABCD có AC là tia phân giác của góc BAD
Suy ra \(\widehat {DAC} = \widehat {CAB}\)
Vì ABCD là hình chữ nhật
Nên \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
Xét tam giác ABC và tam giác ADC có
\(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
AC là cạnh chung
\(\widehat {DAC} = \widehat {CAB}\) (chứng minh trên)
Do đó △ABC = △ADC (cạnh huyền – góc nhọn)
Suy ra AB = AD
Xét hình chữ nhật ABCD có AB = AD
Nên ABCD là hình vuông
Vậy hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.