Chứng minh DI /DA = BC/ (AB + BC + CA)
Cho tam giác ABC có các đường phân giác AD, BE, CF (D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại I. Chứng minh:
DIDA=BCAB+BC+CA;
Cho tam giác ABC có các đường phân giác AD, BE, CF (D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại I. Chứng minh:
DIDA=BCAB+BC+CA;
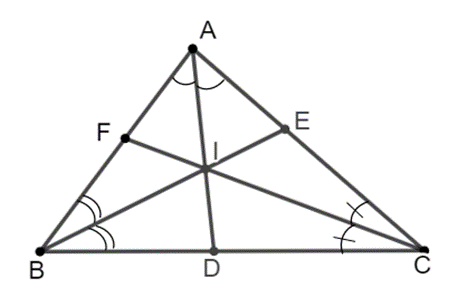
• Vì BI là phân giác của ^ABC trong ∆ABC nên ta có IAID=ABBD.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
IAAB=IDBD=IA+IDAB+BD=ADAB+BD suy ra IDAD=BDAB+BD (1)
• Vì CI là phân giác của ^ACB trong ∆ABC nên ta có IAID=CACD.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
IACA=DICD=IA+IDCA+CD=DACA+CD suy ra DIAD=CDCA+CD (2)
Từ (1) và (2) suy ra: BDAB+BD=CDCA+CD.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
BDAB+BD=CDCA+CD=BD+CDAB+BD+CA+CD=BCAB+BC+CA (3)
Từ (1), (2) và (3) suy ra: DIDA=BCAB+BC+CA.