Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M
Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.
Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.
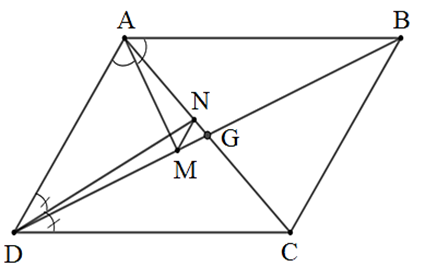
Gọi G là giao điểm của AC và BD.
• Vì DN là phân giác của ^ADC trong ∆ADC nên NANC=ADDC.
• Vì AM là phân giác của ^BAD trong ∆ABD nên MDMB=ADAB= ADDC (vì AB = DC).
Suy ra MDMB=NANC.
Do đó NAMD=NCMB=NA+NCMD+MB=ACBD=AGDG (AC = 2AG; BD = 2BG)
Khi đó NAAG=MDDG.
Xét ∆AGD có NAAG=MDDGnên theo định lí Thalès đảo, ta có MN // AD.