Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Chứng minh

Đề bài: Cho x, y, z là các số thực dương thỏa mãn x + y + z = xyz. Chứng minh

$\frac{1+\sqrt{1+x^2}}{x}+\frac{1+\sqrt{1+y^2}}{y}+\frac{1+\sqrt{1+z^2}}{z}\le xyz$

Trả lời

Hướng dẫn giải:

Áp dụng bất đăng thức Cauchy, ta có $\left\{\begin{array}{l}2xy\le x^2+y^2\\ 2yz\le y^2+z^2\\ 2zx\le z^2+x^2\end{array}\right.$

⇒ 2(xy + yz + zx) ≤ 2(x² + y² + z²)

⇔ xy + yz + zx ≤ x² + y² + z²

⇔ 3(xy + yz + zx) ≤ x² + y² + z² + 2(xy + yz + zx)

⇔ 3(xy + yz + zx) ≤ (x + y + z)²

$\iff xy+yz+zx\le \frac{{\left(x+y+z\right)}^2}{3}$.

Áp dụng bất đẳng thức Cauchy, ta có $\frac{4+\left(1+x^2\right)}{2}\ge \sqrt{4\left(1+x^2\right)}$

Ta có

$\frac{1+\sqrt{1+x^2}}{x}=\frac{2+\sqrt{4\left(1+x^2\right)}}{2x}\le \frac{2+\frac{4+\left(1+x^2\right)}{2}}{2x}=\frac{4+4+\left(1+x^2\right)}{4x}=\frac{9+x^2}{4x}$ .

Chứng minh tương tự, ta có $\frac{1+\sqrt{1+y^2}}{y}\le \frac{9+y^2}{4y}$  và $\frac{1+\sqrt{1+z^2}}{z}\le \frac{9+z^2}{4z}$ .

Khi đó

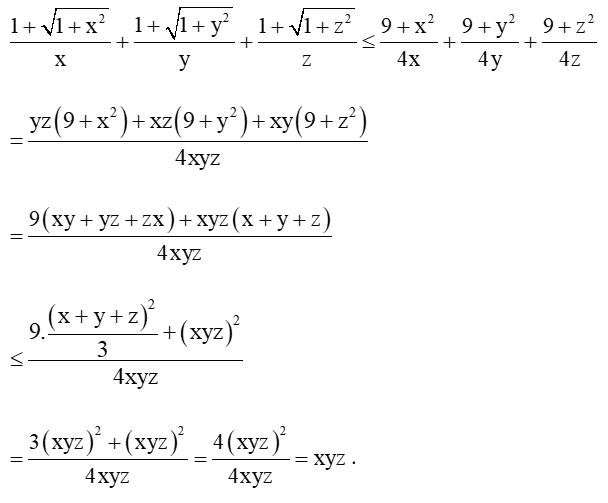
Dấu “=” xảy ra $\iff x=y=z=\sqrt{3}$ .

Vậy ta có điều phải chứng minh.