Cho x, y là hai số thỏa mãn x, y ≥ 1 và 3(x + y) = 4xy

Đề bài: Cho x, y là hai số thỏa mãn x, y ≥ 1 và 3(x + y) = 4xy. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức  P = x^3 + y^3 - 3/(1/x^2 + 1/y^2)

Trả lời

Hướng dẫn giải:

Đặt t = x + y (t ≥ 2).

Theo đề, ta có 3(x + y) = 4xy. Suy ra $xy=\frac{3t}{4}$ .

Theo bất đẳng thức Cauchy, ta có (x + y)² ≥ 4xy.

⇔ (x + y)² ≥ 3(x + y) (theo giả thiết).

⇔ (x + y)² – 3(x + y) ≥ 0.

⇔ (x + y)(x + y – 3) ≥ 0.

⇔ x + y – 3 ≥ 0.

⇔ x + y ≥ 3.

⇔ t ≥ 3.

Mặt khác, vì x, y ≥ 1 nên ta có (x – 1)(y – 1) ≥ 0.

⇔ xy – (x + y) + 1 ≥ 0.

$\iff \frac{3t}{4}-t+1\ge 0$

⇔ t ≤ 4.

Vì vậy ta có 3 ≤ t ≤ 4.

Theo đề, ta có 3(x + y) = 4xy.

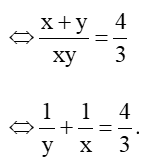
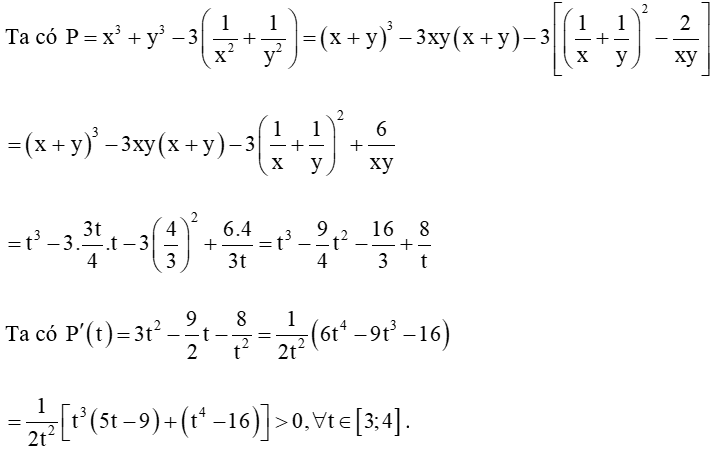
Suy ra hàm số P(t) đồng biến trên [3; 4].

Vậy:

⦁ Giá trị nhỏ nhất của P là $P\left(3\right)=\frac{49}{12}$  khi t = 3 $\iff x=y=\frac{3}{2}$ .

⦁ Giá trị lớn nhất của P là $P\left(4\right)=\frac{74}{3}$  khi t = 4 $\iff \left[\begin{array}{l}x=1\wedge y=3\\ x=3\wedge y=1\end{array}\right.$ .