Cho x, y là các số thực thỏa mãn x > y > 1. Biểu thức A = log x/y ^2 x^3 + 8/3 log y (x/y) đạt giá trị nhỏ nhất khi và chỉ khi
66
16/06/2024
Cho x, y là các số thực thỏa mãn x > y > 1. Biểu thức A=log2xyx3+83logy(xy) đạt giá trị nhỏ nhất khi và chỉ khi
A. x=y4
B. x = y
C. x4=y
D. x = 4y
Trả lời
Chọn A
Ta có
A=log2xyx3+83logy(xy)=9logx2xy+83.[logyx−1]=9(1−logxy)2+83.logxy−83
Đặt logxy=t (logxy>logx1=0⇒t>0 và x>y⇒logxx>logxy⇒1>t)
Suy ra 0 < t < 1.
Khi đó A trở thành: A=9(1−t)2+83t−83=f(t)
Xét hàm số f(t)=9(t−1)2+83t−83 có f'
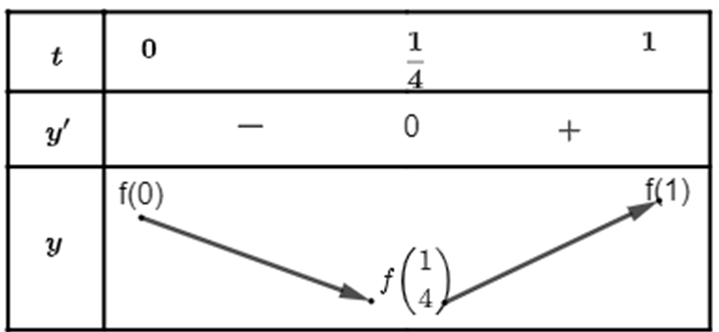
Ta có bảng biến thiên
Vậy A đạt giá trị nhỏ nhất khi