Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = 1. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng OM và AC
58
16/06/2024
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = 1. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng OM và AC bằng 23. Thể tích của khối tứ diện OABC bằng
A. 13.
B. 16.
C. √23.
D. 23.
Trả lời
Chọn A
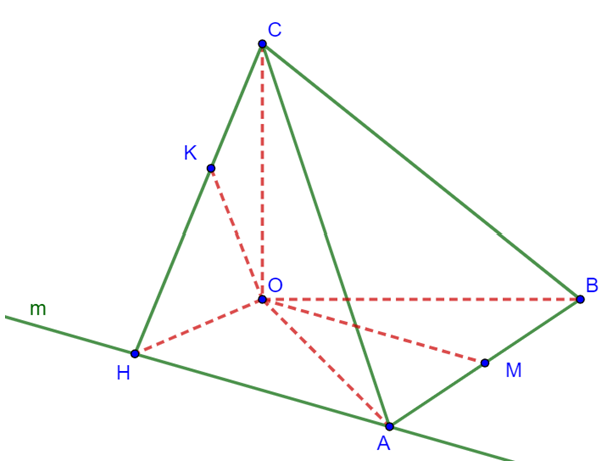
Kẻ Am//OM,OH⊥Am (H∈Am),OK⊥CH(K∈CH) nên d(OM,AC)=d(OM,(CAH))
Ta có: OC⊥(OAB)⇒OC⊥AH,OH⊥AH⇒AH⊥(OCH)⇒AH⊥OK
Mà d(OM,AC)=d(OM,(CAH))=d(O,(CAH))=OK=23.
Vì tam giác OAB cân tại O nên OM⊥AB,OM=AM=AB2.
Vì OH⊥Am⇒OH⊥OM và OM⊥AB,AH//OM⇒AH⊥AM
Nên OHAM là hình vuông ( hình chữ nhật có hai cạnh kề bằng nhau)
Khi đó: OH=AM=AB2=√22.
Do: 1OK2=1OH2+1OC2⇒OC=2⇒VO.ABC=16.OA.OB.OC=13