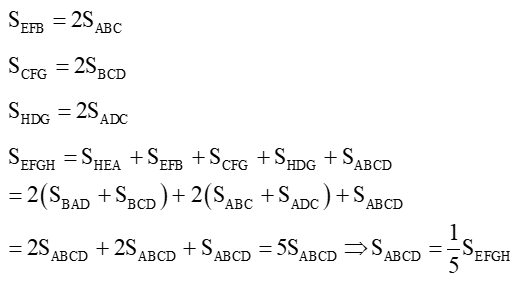Cho tứ giác ABCD. Trên các tia đối của tia BA, CB, DC, AD
Đề bài: Cho tứ giác ABCD. Trên các tia đối của tia BA, CB, DC, AD lần lượt lấy các điểm E, F, G, H sao cho BE = BA, CF = CB, DG = DC và AH = HC. Chứng minh rằng: SABCD=15SEFGH.
Đề bài: Cho tứ giác ABCD. Trên các tia đối của tia BA, CB, DC, AD lần lượt lấy các điểm E, F, G, H sao cho BE = BA, CF = CB, DG = DC và AH = HC. Chứng minh rằng: SABCD=15SEFGH.
Hướng dẫn giải:
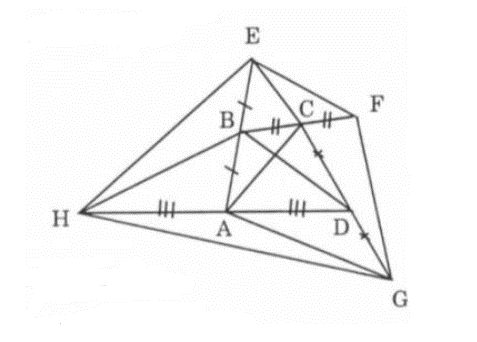
Ta có BA là trung tuyến của tam giác HBD nên diện tích tam giác BAH bằng diện tích tam giác BAD.
HB là trung tuyến của tam giác HEA nên SBAH=SBEH
Do đó SHEA=2SBAD
Chứng minh tương tự có: