Cho tứ giác ABCD. Tìm M nằm trong ABCD sao cho tổng các khoảng cách từ M đến các đỉnh tứ giác nhỏ nhất.

Trả lời

Lời giải

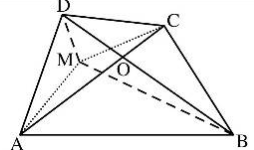
Gọi O là giao điểm của AC và BD

+) Trường hợp 1: O ≡ M

Ta có MA + MB + MC + MD = OA + OB + OC + OD = AC +BD  (1)

+) Trường hợp 2: O ≠ M

Xét tam giác AMC có AC ≤ AM + MC (bất đẳng thức trong tam giác)

Xét tam giác MBD có BD ≤ BM + MB (bất đẳng thức trong tam giác)

Suy ra MA + MB + MC + MD ≥ AC + BD             (2)

Từ (1) và (2) suy ra MA + MB + MC + MD ≥ AC + BD

Dấu “ = ” xảy ra khi O ≡ M

Vậy tổng các khoảng cách từ M đến các đỉnh tứ giác nhỏ nhất khi M là giao điểm của AC và BD.