Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, CD, AD, BC. Chứng minh: vecto MP = vecto QN và vecto MQ = vecto PN

Trả lời

Lời giải

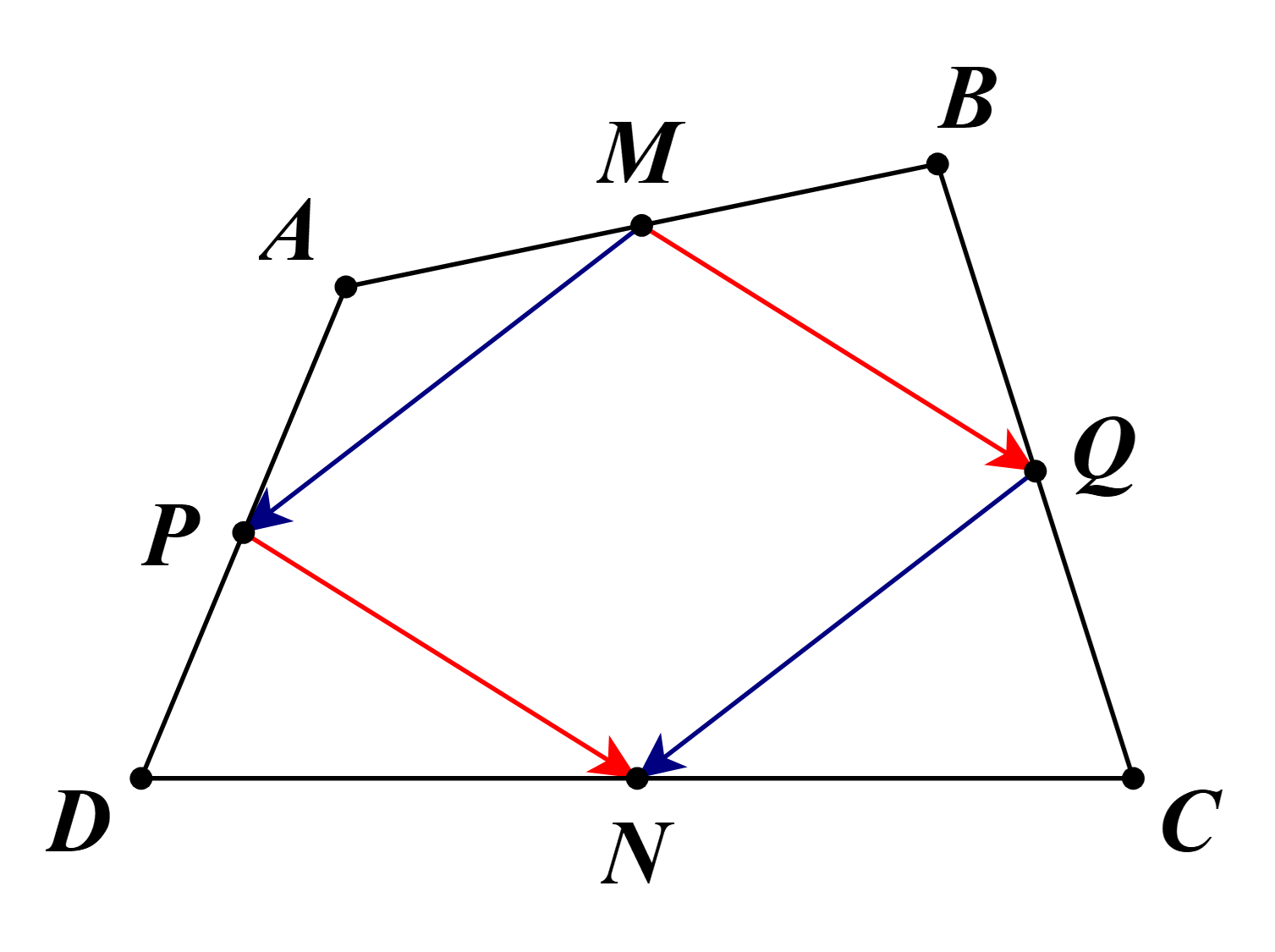
Tam giác ABD có M, P lần lượt là trung điểm của AB, AD.

Suy ra MP là đường trung bình của tam giác ABD.

Do đó \(MP = \frac{1}{2}BD\).

Vì vậy \(\overrightarrow {MP} = \frac{1}{2}\overrightarrow {BD} \)     (1)

Tam giác CBD có Q, N lần lượt là trung điểm của BC, CD.

Suy ra QN là đường trung bình của tam giác CBD.

Do đó \(QN = \frac{1}{2}BD\).

Vì vậy \(\overrightarrow {QN} = \frac{1}{2}\overrightarrow {BD} \)     (2)

Từ (1), (2), suy ra \(\overrightarrow {MP} = \overrightarrow {QN} \).

Chứng minh tương tự ở trên, ta có \(\overrightarrow {MQ} = \overrightarrow {PN} \).

Vậy ta có điều phải chứng minh.