Lời giải

Đáp án đúng là: C

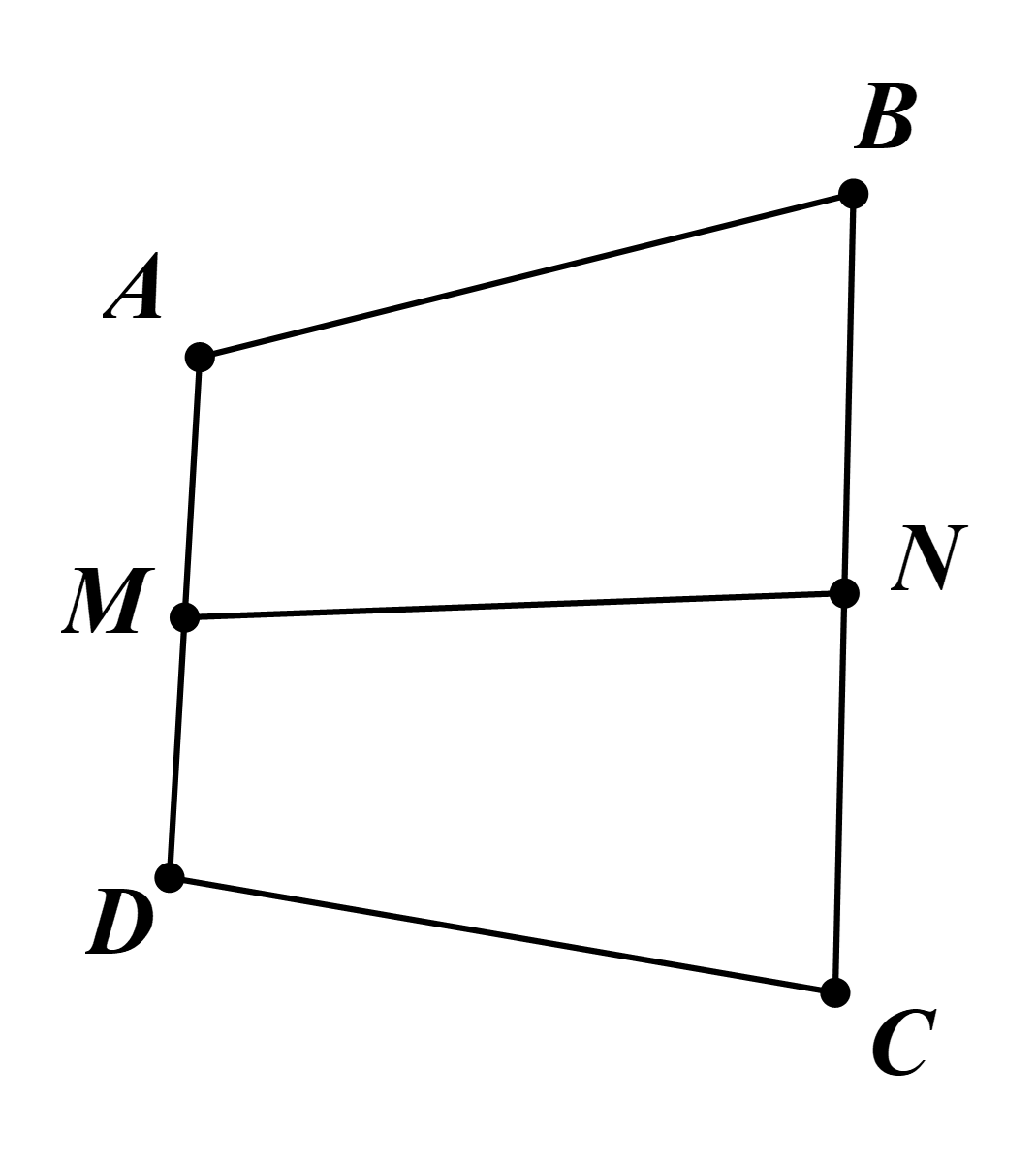
Ta có \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} } \right) + \frac{1}{2}\left( {\overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} } \right)\)

\( = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MD} } \right) + \frac{1}{2}\left( {\overrightarrow {BN} + \overrightarrow {CN} } \right) + \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\) (M, N lần lượt là trung điểm của DA, BC).

\( = \frac{1}{2}.\vec 0 + \frac{1}{2}.\vec 0 + \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right) = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).

Suy ra \(M{N^2} = \frac{1}{4}\left( {A{B^2} + D{C^2} + 2\overrightarrow {AB} .\overrightarrow {DC} } \right)\)

\( \Leftrightarrow 3{a^2} = \frac{1}{4}\left( {4{a^2} + 4{a^2} + 2\overrightarrow {AB} .\overrightarrow {DC} } \right)\)

\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {DC} = 2{a^2}\).

Ta có \(\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {DC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DC} }}{{AB.DC}} = \frac{{2{a^2}}}{{2a.2a}} = \frac{1}{2}\).

Suy ra \(\left( {\overrightarrow {AB} ,\,\overrightarrow {DC} } \right) = 60^\circ \).

Vậy góc giữa hai đường thẳng AB và CD bằng 60°.