Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA

Bài 3 trang 65 Toán 8 Tập 2: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a) Chứng minh tứ giác MNPQ là hình bình hành.

b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

c) Cho AC ⊥ BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

Trả lời

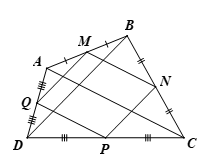
a) Xét ∆ABC có M, N lần lượt là trung điểm AB, BC nên MN là đường trung bình của ∆ABC

Suy ra MN//AC và $\mathrm{MN}=\frac{1}{2}\mathrm{AC}$ (1)

Xét ∆ADC có P, Q lần lượt là trung điểm DC, AD nên PQ là đường trung bình của ∆ADC

Suy ra PQ//AC và $\mathrm{PQ}=\frac{1}{2}\mathrm{AC}$ (2)

Từ (1) và (2) suy ra MN // PQ; MN = PQ.

Tứ giác MNPQ có MN // PQ; MN = PQ nên MNPQ là hình bình hành.

b) Xét tam giác ABD có M, Q lần lượt là trung điểm AB, AD nên MQ là đường trung bình của ∆ABD

Suy raMQ // BD và $\mathrm{MQ}=\frac{1}{2}\mathrm{BD}$

Mà $\mathrm{MN}=\frac{1}{2}\mathrm{AC}$ và AC = BD nên MN = MQ.

Hình bình hành MNPQ có MN = MQ nên MNPQ là hình thoi.

c) Ta có MN // AC (câu a), MQ // BD (câu b) và AC ⊥ BD (giả thiết)

Suy ra MN ⊥ MQ hay $\widehat{\mathrm{NMQ}}=90°$

Hình bình hành MNPQ có $\widehat{\mathrm{NMQ}}=90°$ nên là hình chữ nhật.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 1: Định lí Thalès trong tam giác

Bài 2: Ứng dụng của định lí Thalès trong tam giác

Bài 3: Đường trung bình của tam giác

Bài 4: Tính chất đường phân giác của tam giác

Bài 5: Tam giác đồng dạng

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác