Bài 2 trang 65 Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:
a) MN // CP;
b) AQ = QM;
c) CP = 4PQ.
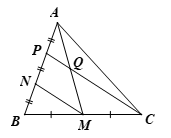
a) Do PN = NB nên N là trung điểm của BP.
Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.
Xét ∆BCP có M, N lần lượt là trung điểm của BC, BP nên MN là đường trung bình của ∆BCP
Suy ra MN // CP.
b) Do AP = PN nên P là trung điểm của AN.
Mà MN // CP, Q ∈ CP nên MN // PQ.
Xét ∆AMN có PQ đi qua P là trung điểm của AN và PQ // MN
Suy ra Q là trung điểm của AM nên AQ = QM.
c) Xét ∆AMN có P, Q lần lượt là trung điểm của AN, AM nên là đường trung bình của ∆AMN. Do đó
Lại có MN là đường trung bình của ∆BCP nên
Khi đó
Suy ra CP = 4PQ.
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:
Bài 1: Định lí Thalès trong tam giác
Bài 2: Ứng dụng của định lí Thalès trong tam giác
Bài 3: Đường trung bình của tam giác