Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC

Câu 34: Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.

Trả lời

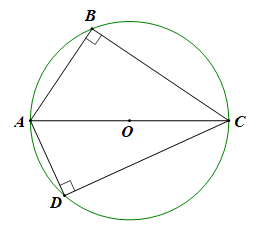
Xét ∆ABC có: $\widehat{ABC}={90}^{\text{o}}$  (gt)

Suy ra AC là cạnh huyền.

Lại có: AO = OC (gt)

⇒ BO là đường trung tuyến ∆ABC

⇒ BO = AO = OC (đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền) (1)

Tương tự ta chứng minh được: DO = AO = OC (2)

Từ (1) và (2) ta có: BO = AO = OC = DO

Suy ra 4 điểm A, B, C, D cùng thuộc đường trong đường kính AC.