Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và góc OAD = góc OCB

Luyện tập 2 trang 107 Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và $\widehat{OAD}=\widehat{OCB}$. Chứng minh tứ giác ABCD là hình bình hành.

Trả lời

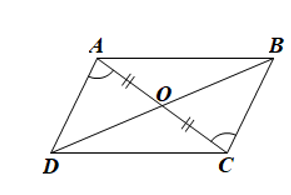
• Xét ΔOAD và ΔOCB có:

$\widehat{OAD}=\widehat{OCB}$ (giả thiết);

OA = OC (giả thiết);

$\widehat{AOD}=\widehat{COB}$ (đối đỉnh)

Do đó ΔOAD = ΔOCB (g.c.g)

Suy ra OD = OB (hai cạnh tương ứng)

• Xét tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường

Do đó ABCD là hình bình hành.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành