Cho tứ giác ABCD có góc D + góc C = 90 độ . Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA

Đề bài. Cho tứ giác ABCD có $\widehat{D}+\widehat{C}={90}^{\circ }$. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA. Chứng minh rằng bốn điểm M, N, P, Q cùng nằm trên một đường tròn.

Trả lời

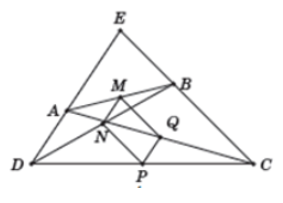Giả sử AD cắt BC tại E

Khi đó từ giả thiết: $\widehat{D}+\widehat{C}={90}^{\circ }$ ta có: $\widehat{E}={180}^{\circ }\mathrm{ }-(\widehat{C}+\widehat{D})={90}^{\circ }$

Ta lần lượt có: MN // AD // PQ; MQ // BC // PN

Do đó dựa trên tính chất của góc có cạnh tương ứng song song ta được:

$\widehat{MNQ}=\widehat{NPQ}=\widehat{E}={90}^{\circ }$

Do đó bốn điểm M, N, P, Q cùng nằm trên một đường tròn đường kính NQ.