Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC và BD. Đường thẳng EF lần lượt cắt AB, CD tại H, K. Chứng minh rằng góc KHB = góc HKC

Trả lời

Lời giải

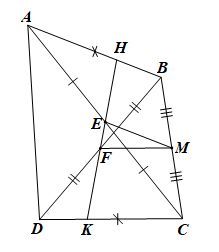
Gọi M là trung điểm của BC.

Xét DABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác

Suy ra EM // DC và \(EM = \frac{1}{2}AB\).

Chứng minh tương tự ta cũng có: FM là đường trung bình của tam giác BCD.

Suy ra FM // DC và \(FM = \frac{1}{2}DC\)

Mà theo bài, AB = CD nên EM = FM

Do đó tam giác EFM là tam giác cân tại M, suy ra \(\widehat {FEM} = \widehat {EFM}\).

Mặt khác, do EM // AB nên \(\widehat {FEM} = \widehat {KHB}\) (đồng vị);

                      FM // DC nên \(\widehat {EFM} = \widehat {HKC}\) (đồng vị).

Do đó \(\widehat {KHB} = \widehat {HKC}\) (điều phải chứng minh).