Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC

Bài 13 trang 106 Toán 11 Tập 2: Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp B.CMND bằng

A. $\frac{a^3\sqrt{2}}{12}$ .

B. $\frac{a^3\sqrt{2}}{16}$ .

C. $\frac{a^3\sqrt{2}}{24}$ .

D. $\frac{a^3\sqrt{2}}{8}$ .

Trả lời

Đáp án đúng là: B

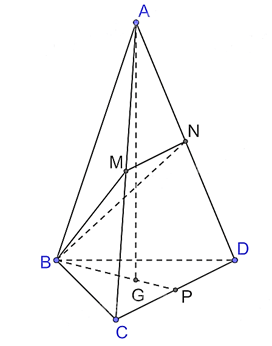
Gọi G là tâm của tam giác BCD. Vì tứ diện ABCD đều nên G là trọng tâm đồng thời là trực tâm của tam giác BCD và AG $\perp$ (BCD).

Kẻ BG cắt CD tại P, suy ra P là trung điểm của CD và BG = $\frac{2}{3}$BP .

Xét tam giác BCD đều cạnh a có BP là đường cao nên BP = $\frac{a\sqrt{3}}{2}$ , suy ra BG = $\frac{a\sqrt{3}}{3}$ .

Xét tam giác ABG vuông tại G, có AG = $\sqrt{A{B}^2-B{G}^2}=\sqrt{a^2-\frac{a^2}{3}}=\frac{a\sqrt{6}}{3}$ .

Vì tam giác BCD đều cạnh a nên $S_{BCD}=\frac{a^2\sqrt{3}}{4}$ .

Ta có $V_{ABCD}=\frac{1}{3}\cdot S_{BCD}\cdot AG$$=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{4}\cdot \frac{a\sqrt{6}}{3}$$=\frac{a^3\sqrt{2}}{12}$ .

Vì M, N lần lượt là trung điểm của cạnh AC và cạnh AD nên $\frac{AM}{AC}=\frac{AN}{AD}=\frac{1}{2}$ .

Có $\frac{V_{A.BMN}}{V_{A.BCD}}=\frac{AB}{AB}\cdot \frac{AM}{AC}\cdot \frac{AN}{AD}$$=1\cdot \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$$\Rightarrow V_{A.BMN}=\frac{1}{4}{V}_{A.BCD}$ .

Mà V_A.BMN + V_B.CMND = V_ABCD nên $V_{B.CMND}=\frac{3}{4}{V}_{ABCD}$$=\frac{3}{4}\cdot \frac{a^3\sqrt{2}}{12}=\frac{a^3\sqrt{2}}{16}$.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: