Lời giải
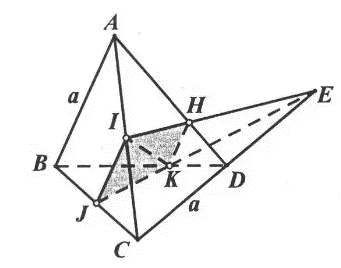
Gọi E là giao điểm của JK và CD, H là giao điểm của EI và AD
Suy ra thiết diện của tứ diện cắt bởi mặt phẳng (IJK) là tứ giác IJKH
Xét tam giác ABC có I,J lần lượt là trung điểm của AC, BC
Nên IJ là đường trung bình
Suy ra IJ // AB
Ta có AB ⊂ (ABD), IJ ⊂ (IJK), AB // IJ (chứng minh trên)
Suy ra (ABD) ∩ (IJK) = HK // AB // IJ
Do đó IJKH là hình thang (1)
Vì ABCD là tứ diện đều (giả thiết) nên AC = BC, \(\widehat {CBD} = \widehat {CA{\rm{D}}}\), AD = BD
Ta có AC = BC, AC = 2AI, BC = 2BJ
Suy ra AI = BJ
Xét tam giác ABD có HK // AB và BK = 2KD
Suy ra AH = 2 HD
Mà AD = BD nên AH = BK
Xét tam giác AHI và tam giác BKJ có
AH = BK (chứng minh trên)
\(\widehat {KBJ} = \widehat {HAI}\) (chứng minh trên)
AI = BJ (chứng minh trên)
Do đó △AHI = △BKJ (c.g.c)
Suy ra HI = KJ (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có IJKH là hình thang cân
Vậy thiết diện của tứ diện cắt bởi mặt phẳng (IJK) là hình thang cân.