Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC. Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó
203
07/12/2023
Bài 3 trang 51 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC.
a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó.
b) Chứng minh hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.
Trả lời
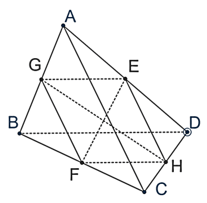
a) Gọi E, F lần lượt là trung điểm của các cạnh AD, BC.
Xét ∆BAD và ∆CDA, ta có:

Do đó ∆BAD = ∆CDA (c.c.c)
Ta có BE = CE (2 đường trung tuyến ứng với cạnh AD).
Suy ra ∆BEC cân tại E nên EF ⊥ BC.
Chứng minh tương tự, ta có: EF ⊥ AD.
Vậy đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó.
b)Gọi G, H lần lượt là các trung điểm của 2 cạnh AB và CD.
Theo tính chất đường trung bình, ta có:
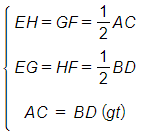 EH = GF = EG = HF
EH = GF = EG = HF
Khi đó, EHFG là hình thoi, suy ra EF ⊥ GH.
Vậy hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:



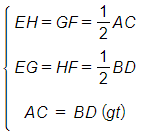 EH = GF = EG = HF
EH = GF = EG = HF