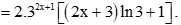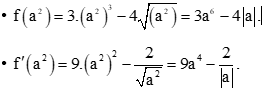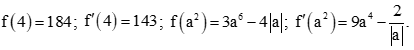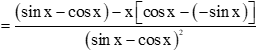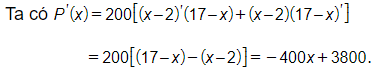Sách bài tập Toán 11 Bài 2: Các quy tắc tính đạo hàm
Bài 1 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y=−3x22+2x+x33;
b) y = (x2 − 1)(x2 – 4)(x2 + 9);
c) y=x2−2xx2+x+1;
d) y=1−2xx+1;
e) y = xe2x + 1;
g) y = (2x + 3)32x + 1;
h) y = xln2x;
i) y=log2(x2+1).
Lời giải:
a) y'.
b) y = (x2 − 1)(x2 – 4)(x2 + 9)
= (x4 – 5x2 + 4)(x2 + 9)
= x6 – 5x4 + 4x2 + 9x4 – 45x2 + 36
= x6 + 4x4 – 41x2 + 36.
y' = 6x5 + 16x3 – 82x
c)
.
d)
e)
.
g)
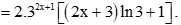
h)
.
i) .
Bài 2 trang 43 SBT Toán 11 Tập 2: Cho hàm số . Tính (a là hằng số khác 0).
Lời giải:
Ta có .
• .
• .
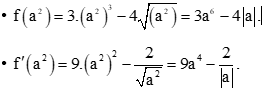
Vậy 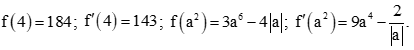
Bài 3 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = (1 + x2)20;
b) .
Lời giải:
a) .
b)
.
Bài 4 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) ;
b) ;
c) ;
d) y = cos (2sinx).
Lời giải:
a)
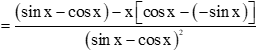
.
b)
c)
.
d)
Bài 5 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm cấp 2 của các hàm số sau:
a) y = xsin 2x;
b) y = cos2x;
c) y = x4 – 3x3 + x2 − 1.
Lời giải:
a)
.
b)
.
c) .
.
Bài 6 trang 43 SBT Toán 11 Tập 2: Một chất điểm chuyển động thẳng có phương trình s = 100 + 2t – t2 trong đó thời gian được tính bằng giây và s được tính bằng mét.
a) Tại thời điểm nào chất điểm có vận tốc bằng 0?
b) Tìm vận tốc và gia tốc của chất điểm tại thời điểm t = 3s.
Lời giải:
Ta có , suy ra .
a) Vận tốc chất điểm bằng 0 khi hay t = 1
Vậy vận tốc chất điểm bằng 0 khi t = 1 s.
b) Khi t = 3s, ta có:
• (m/s);
• (m/s2).
Vậy khi t = 3 s thì vận tốc của chất điểm là −4 m/s; gia tốc của chất điểm là −2 m/s2.
Bài 7 trang 44 SBT Toán 11 Tập 2: Một chuyển động thẳng xác định bởi phương trình s(t) = −2t3 + 75t + 3, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc và gia tốc của chuyển động tại thời điểm t =3
Lời giải:
Ta có , suy ra .
• (m/s).
• (m/s2).
Vậy tại thời điểm t = 3 vận tốc của chuyển động là 21 (m/s) và gia tốc của chuyển động là −36 (m/s2).
Bài 8 trang 44 SBT Toán 11 Tập 2: Nếu số lượng sản phẩm sản xuất được của một nhà máy là x (đơn vị: trăm sản phẩm) thì lợi nhuận sinh ra là P(x) = 200(x – 2)(17 – x) (nghìn đồng). Tính tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm
Lời giải:
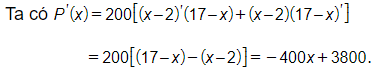
Vậy tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm là –8200 nghìn đồng.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: