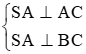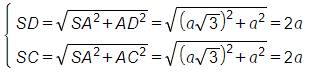Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = a Căn 3, SA vuông góc với AC, SA vuông góc với BC, góc BAD = 120 độ
2.6k
07/12/2023
Bài 2 trang 51 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = a√3, SA ⊥ AC, SA ⊥ BC, ^BAD= 120°. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:
a) SD và BC.
b) MN và SC.
Trả lời
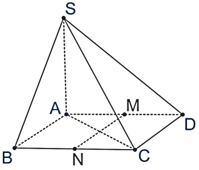
a) Ta có: 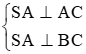
⇒ SA ⊥ (ABCD) ⇔ SA ⊥ AD.
Do BC // AD nên (BC, SD) = (AD, SD).
tan^ADS=SAAD=a√3a=√3
Do đó (BC,SD)=^ADS = 60°.
b) Do MN // CD nên (SD, MN) = (SD, CD) = ^SCD .
Áp dụng định lí Pythagore, ta có:
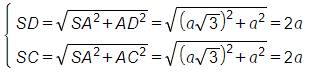
Áp dụng định lí hàm cos trong ∆SCD, ta có:
cos^SCD=SC2+CD2−SD22 . SC . CD=(2a)2+a2−(2a)22 . 2 . a . a=14.
Do đó (SD, MN) = ≈ 75,52°.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: