Câu hỏi:
03/04/2024 50
Cho tứ diện ABCD có \[AB = BC = AC = CD = DB = a,AD = \frac{{a\sqrt 3 }}{2}\]. Gọi M là trung điểm của AB, điểm O là tâm đường tròn ngoại tiếp tam giác BCD. Đường thẳng AO cắt mặt phẳng \[\left( {MCD} \right)\] tại G. Tính diện tích tam giác GAD.
Cho tứ diện ABCD có \[AB = BC = AC = CD = DB = a,AD = \frac{{a\sqrt 3 }}{2}\]. Gọi M là trung điểm của AB, điểm O là tâm đường tròn ngoại tiếp tam giác BCD. Đường thẳng AO cắt mặt phẳng \[\left( {MCD} \right)\] tại G. Tính diện tích tam giác GAD.
A. \[\frac{{\sqrt 3 {a^2}}}{{32}}\].
B. \[\frac{{3\sqrt 3 {a^2}}}{{32}}\].
C. \[\frac{{3\sqrt 3 {a^2}}}{{16}}\].
D. \[\frac{{\sqrt 3 {a^2}}}{{16}}\].
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp
Tính độ dài các đoạn GA, GD, AD rồi nhận xét tính chất tam giác GAD.
Cách giải
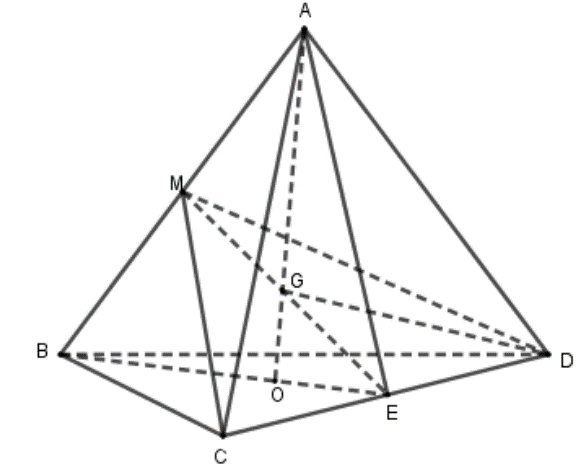
Tam giác ACD có \[AC = CD = a,AD = \frac{{a\sqrt 3 }}{2}\] nên \[A{E^2} = \frac{{A{C^2} + A{D^2}}}{2} - \frac{{C{D^2}}}{4} = \frac{{{a^2} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác BCD đều \[ \Rightarrow BE = \frac{{a\sqrt 3 }}{2}\].
Tam giác ABE có EM là đường trung tuyến của tam giác AEB nên:
\[E{M^2} = \frac{{E{A^2} + E{B^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{\frac{{5{a^2}}}{8} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{7{a^2}}}{{16}}\].
Xét tam giác BME và bộ ba điểm A, G, O thẳng hàng có: \[\frac{{AM}}{{AB}}.\frac{{OB}}{{OE}}.\frac{{GE}}{{GM}} = 1 \Rightarrow \frac{1}{2}.2.\frac{{GE}}{{GM}} = 1 \Leftrightarrow \frac{{GE}}{{GM}} = 1\] hay G là trung điểm của ME.
Xét tam giác ABD có DM là trung tuyến của \[\Delta ABD\] nên \[D{M^2} = \frac{{D{A^2} + B{D^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác DME có trung tuyến DG nên \[D{G^2} = \frac{{D{E^2} + D{M^2}}}{2} - \frac{{M{E^2}}}{4} = \frac{{\frac{{{a^2}}}{4} + \frac{{5{a^2}}}{8}}}{2} - \frac{{7{a^2}}}{{64}} = \frac{{21{a^2}}}{{64}}\].
Lại có: \[\begin{array}{l}\cos AEM = \frac{{A{E^2} + E{M^2} - A{M^2}}}{{2.AE.EM}} = \frac{{\frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{16}} - \frac{{{a^2}}}{4}}}{{2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{16}}} }} = \frac{{13}}{{2\sqrt {70} }}\\ \Rightarrow A{G^2} = A{E^2} + E{G^2} - 2AE.EG.\cos AEG = \frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{64}} - 2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{64}}} .\frac{{13}}{{2\sqrt {70} }} = \frac{{21{a^2}}}{{64}}\end{array}\]
Tam giác ADG có \[A{G^2} = \frac{{21{a^2}}}{{64}},A{D^2} = \frac{{3{a^2}}}{4},D{G^2} = \frac{{21{a^2}}}{{64}}\].
Do đó \[\Delta GAD\] cân tại G.
Gọi H là trung điểm của AD thì \[AH = \frac{{a\sqrt 3 }}{4},G{H^2} = G{A^2} - A{H^2} = \frac{{21{a^2}}}{{64}} - \frac{{3{a^2}}}{{16}} = \frac{{9{a^2}}}{{64}} \Rightarrow GH = \frac{{3a}}{8}\].
Diện tích tam giác \[{S_{GAD}} = \frac{1}{2}.GH.AD = \frac{1}{2}.\frac{{3a}}{8}.\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 3 }}{{32}}\].
Đáp án B
Phương pháp
Tính độ dài các đoạn GA, GD, AD rồi nhận xét tính chất tam giác GAD.
Cách giải

Tam giác ACD có \[AC = CD = a,AD = \frac{{a\sqrt 3 }}{2}\] nên \[A{E^2} = \frac{{A{C^2} + A{D^2}}}{2} - \frac{{C{D^2}}}{4} = \frac{{{a^2} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác BCD đều \[ \Rightarrow BE = \frac{{a\sqrt 3 }}{2}\].
Tam giác ABE có EM là đường trung tuyến của tam giác AEB nên:
\[E{M^2} = \frac{{E{A^2} + E{B^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{\frac{{5{a^2}}}{8} + \frac{{3{a^2}}}{4}}}{2} - \frac{{{a^2}}}{4} = \frac{{7{a^2}}}{{16}}\].
Xét tam giác BME và bộ ba điểm A, G, O thẳng hàng có: \[\frac{{AM}}{{AB}}.\frac{{OB}}{{OE}}.\frac{{GE}}{{GM}} = 1 \Rightarrow \frac{1}{2}.2.\frac{{GE}}{{GM}} = 1 \Leftrightarrow \frac{{GE}}{{GM}} = 1\] hay G là trung điểm của ME.
Xét tam giác ABD có DM là trung tuyến của \[\Delta ABD\] nên \[D{M^2} = \frac{{D{A^2} + B{D^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{5{a^2}}}{8}\].
Tam giác DME có trung tuyến DG nên \[D{G^2} = \frac{{D{E^2} + D{M^2}}}{2} - \frac{{M{E^2}}}{4} = \frac{{\frac{{{a^2}}}{4} + \frac{{5{a^2}}}{8}}}{2} - \frac{{7{a^2}}}{{64}} = \frac{{21{a^2}}}{{64}}\].
Lại có: \[\begin{array}{l}\cos AEM = \frac{{A{E^2} + E{M^2} - A{M^2}}}{{2.AE.EM}} = \frac{{\frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{16}} - \frac{{{a^2}}}{4}}}{{2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{16}}} }} = \frac{{13}}{{2\sqrt {70} }}\\ \Rightarrow A{G^2} = A{E^2} + E{G^2} - 2AE.EG.\cos AEG = \frac{{5{a^2}}}{8} + \frac{{7{a^2}}}{{64}} - 2.\sqrt {\frac{{5{a^2}}}{8}.\frac{{7{a^2}}}{{64}}} .\frac{{13}}{{2\sqrt {70} }} = \frac{{21{a^2}}}{{64}}\end{array}\]
Tam giác ADG có \[A{G^2} = \frac{{21{a^2}}}{{64}},A{D^2} = \frac{{3{a^2}}}{4},D{G^2} = \frac{{21{a^2}}}{{64}}\].
Do đó \[\Delta GAD\] cân tại G.
Gọi H là trung điểm của AD thì \[AH = \frac{{a\sqrt 3 }}{4},G{H^2} = G{A^2} - A{H^2} = \frac{{21{a^2}}}{{64}} - \frac{{3{a^2}}}{{16}} = \frac{{9{a^2}}}{{64}} \Rightarrow GH = \frac{{3a}}{8}\].
Diện tích tam giác \[{S_{GAD}} = \frac{1}{2}.GH.AD = \frac{1}{2}.\frac{{3a}}{8}.\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 3 }}{{32}}\].
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho các hình vẽ sau:

Trong các hình trên, hình nào có trục đối xứng và đồng thời có tâm đối xứng?
Cho các hình vẽ sau:

Trong các hình trên, hình nào có trục đối xứng và đồng thời có tâm đối xứng?
Câu 5:
Đề kiểm tra một tiết môn toán của lớp 12A có 25 câu trắc nghiệm, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án đúng. Một học sinh không học bài nên làm bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó làm đúng đáp án 15 câu.
Câu 6:
Khai triển đa thức \[P\left( x \right) = {\left( {\frac{1}{3} + \frac{2}{3}x} \right)^{10}} = {a_0} + {a_1}x + ... + {a_9}{x^9} + {a_{10}}{x^{10}}\]. Tìm hệ số \[{a_k}\left( {0 \le k \le 10;k \in \mathbb{N}} \right)\] lớn nhất trong khai triển trên.
Câu 7:
Tính giá trị của tổng \[T = C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{2018}\].
Câu 8:
Cho hai đường tròn bằng nhau \[\left( {I;R} \right)\] và \[\left( {I';R'} \right)\] với tâm I và I’ phân biệt. Có bao nhiêu phép vị tự biến \[\left( {I;R} \right)\] thành \[\left( {I';R'} \right)\]?
Câu 9:
Có bao nhiêu số tự nhiên có sáu chữ số sao cho trong mỗi số đó chữ số sau lớn hơn chữ số trước?
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AB//CD,AB = 2CD} \right)\]. Gọi M là trung điểm của cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
b) Xác định giao điểm K của đường thẳng AM với \[mp\left( {SBD} \right)\]. Tính tỉ số \[\frac{{AK}}{{AM}}\].
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AB//CD,AB = 2CD} \right)\]. Gọi M là trung điểm của cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
b) Xác định giao điểm K của đường thẳng AM với \[mp\left( {SBD} \right)\]. Tính tỉ số \[\frac{{AK}}{{AM}}\].


