Câu hỏi:
03/04/2024 53
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AB//CD,AB = 2CD} \right)\]. Gọi M là trung điểm của cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
b) Xác định giao điểm K của đường thẳng AM với \[mp\left( {SBD} \right)\]. Tính tỉ số \[\frac{{AK}}{{AM}}\].
Cho hình chóp S.ABCD có đáy ABCD là hình thang \[\left( {AB//CD,AB = 2CD} \right)\]. Gọi M là trung điểm của cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
b) Xác định giao điểm K của đường thẳng AM với \[mp\left( {SBD} \right)\]. Tính tỉ số \[\frac{{AK}}{{AM}}\].
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp
a) Sử dụng định lí \[\left\{ \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a//b\end{array} \right. \Rightarrow d//a//b\]
b) Phương pháp xác định giao điểm của đường thẳng với mặt phẳng:
- Tìm mặt phẳng phụ \[\left( P \right)\] chứa đường thẳng a.
- Tìm giao tuyến d của \[\left( P \right)\] với \[\left( \alpha \right)\] đã cho.
- Tìm giao điểm của d với a.
Sử dụng định lí Ta-let suy ra tỉ số.
Cách giải
a) Xác định giao tuyến của hai mặt phẳng \[\left( {{\bf{SAB}}} \right)\] và \[\left( {{\bf{SCD}}} \right)\].
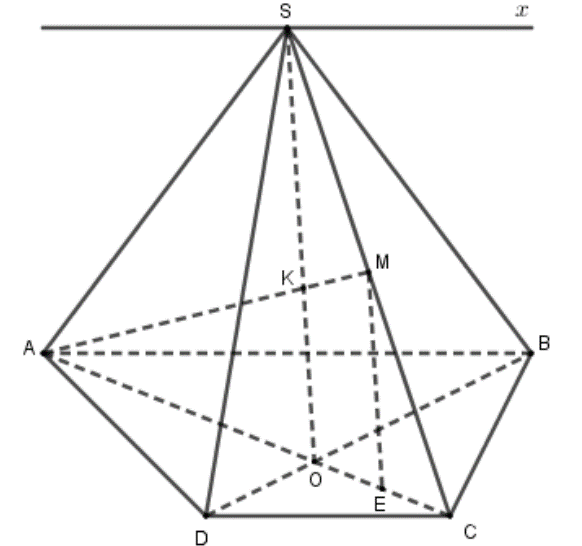
S là điểm chung của \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
\[AB//CD;AB \subset \left( {SAB} \right);CD \subset \left( {SCD} \right)\].
Suy ra \[\left( {SAB} \right) \cap \left( {SCD} \right) = Sx//AB//CD\].
b) Xác định giao điểm K của đường thẳng AM với \[{\bf{mp}}\left( {{\bf{SBD}}} \right)\]. Tính tỉ số \[\frac{{{\bf{AK}}}}{{{\bf{AM}}}}\].
Ta có: \[AM \subset \left( {SAC} \right)\]
Dễ thấy \[S \in \left( {SAC} \right) \cap \left( {SBD} \right)\].
Gọi O là giao điểm của AC và BD. Khi đó \[O \in AC \subset \left( {SAC} \right),O \in BD \subset \left( {SBD} \right)\] nên \[O \in \left( {SAC} \right) \cap \left( {SBD} \right)\]
Do đó \[SO = \left( {SAC} \right) \cap \left( {SBD} \right)\]
Trong \[\left( {SAC} \right)\], gọi \[K = AM \cap SO\] thì \[K \in AM,K \in SO \subset \left( {SBD} \right)\] nên \[K = AM \cap \left( {SBD} \right)\].
Do \[AB//CD\] nên \[\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{1}{2} \Rightarrow OA = \frac{2}{3}AC,OC = \frac{1}{3}AC\].
Gọi E là trung điểm của OC suy ra ME là đường trung bình của \[\Delta SCO \Rightarrow ME//SO\].
Mà \[OE = \frac{1}{2}OC = \frac{1}{2}.\frac{1}{3}.AC = \frac{1}{6}.AC \Rightarrow AE = AO + OE = \frac{2}{3}AC + \frac{1}{6}AC = \frac{5}{6}AC\].
\[ \Rightarrow \frac{{AK}}{{AM}} = \frac{{AO}}{{AE}} = \frac{4}{5}\].
Phương pháp
a) Sử dụng định lí \[\left\{ \begin{array}{l}a \subset \left( P \right)\\b \subset \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a//b\end{array} \right. \Rightarrow d//a//b\]
b) Phương pháp xác định giao điểm của đường thẳng với mặt phẳng:
- Tìm mặt phẳng phụ \[\left( P \right)\] chứa đường thẳng a.
- Tìm giao tuyến d của \[\left( P \right)\] với \[\left( \alpha \right)\] đã cho.
- Tìm giao điểm của d với a.
Sử dụng định lí Ta-let suy ra tỉ số.
Cách giải
a) Xác định giao tuyến của hai mặt phẳng \[\left( {{\bf{SAB}}} \right)\] và \[\left( {{\bf{SCD}}} \right)\].

S là điểm chung của \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\].
\[AB//CD;AB \subset \left( {SAB} \right);CD \subset \left( {SCD} \right)\].
Suy ra \[\left( {SAB} \right) \cap \left( {SCD} \right) = Sx//AB//CD\].
b) Xác định giao điểm K của đường thẳng AM với \[{\bf{mp}}\left( {{\bf{SBD}}} \right)\]. Tính tỉ số \[\frac{{{\bf{AK}}}}{{{\bf{AM}}}}\].
Ta có: \[AM \subset \left( {SAC} \right)\]
Dễ thấy \[S \in \left( {SAC} \right) \cap \left( {SBD} \right)\].
Gọi O là giao điểm của AC và BD. Khi đó \[O \in AC \subset \left( {SAC} \right),O \in BD \subset \left( {SBD} \right)\] nên \[O \in \left( {SAC} \right) \cap \left( {SBD} \right)\]
Do đó \[SO = \left( {SAC} \right) \cap \left( {SBD} \right)\]
Trong \[\left( {SAC} \right)\], gọi \[K = AM \cap SO\] thì \[K \in AM,K \in SO \subset \left( {SBD} \right)\] nên \[K = AM \cap \left( {SBD} \right)\].
Do \[AB//CD\] nên \[\frac{{OC}}{{OA}} = \frac{{CD}}{{AB}} = \frac{1}{2} \Rightarrow OA = \frac{2}{3}AC,OC = \frac{1}{3}AC\].
Gọi E là trung điểm của OC suy ra ME là đường trung bình của \[\Delta SCO \Rightarrow ME//SO\].
Mà \[OE = \frac{1}{2}OC = \frac{1}{2}.\frac{1}{3}.AC = \frac{1}{6}.AC \Rightarrow AE = AO + OE = \frac{2}{3}AC + \frac{1}{6}AC = \frac{5}{6}AC\].
\[ \Rightarrow \frac{{AK}}{{AM}} = \frac{{AO}}{{AE}} = \frac{4}{5}\].
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho các hình vẽ sau:

Trong các hình trên, hình nào có trục đối xứng và đồng thời có tâm đối xứng?
Cho các hình vẽ sau:

Trong các hình trên, hình nào có trục đối xứng và đồng thời có tâm đối xứng?
Câu 5:
Đề kiểm tra một tiết môn toán của lớp 12A có 25 câu trắc nghiệm, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án đúng. Một học sinh không học bài nên làm bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó làm đúng đáp án 15 câu.
Câu 6:
Khai triển đa thức \[P\left( x \right) = {\left( {\frac{1}{3} + \frac{2}{3}x} \right)^{10}} = {a_0} + {a_1}x + ... + {a_9}{x^9} + {a_{10}}{x^{10}}\]. Tìm hệ số \[{a_k}\left( {0 \le k \le 10;k \in \mathbb{N}} \right)\] lớn nhất trong khai triển trên.
Câu 7:
Tính giá trị của tổng \[T = C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{2018}\].
Câu 8:
Cho hai đường tròn bằng nhau \[\left( {I;R} \right)\] và \[\left( {I';R'} \right)\] với tâm I và I’ phân biệt. Có bao nhiêu phép vị tự biến \[\left( {I;R} \right)\] thành \[\left( {I';R'} \right)\]?
Câu 9:
Có bao nhiêu số tự nhiên có sáu chữ số sao cho trong mỗi số đó chữ số sau lớn hơn chữ số trước?
Câu 11:
Cho tứ diện ABCD có \[AB = BC = AC = CD = DB = a,AD = \frac{{a\sqrt 3 }}{2}\]. Gọi M là trung điểm của AB, điểm O là tâm đường tròn ngoại tiếp tam giác BCD. Đường thẳng AO cắt mặt phẳng \[\left( {MCD} \right)\] tại G. Tính diện tích tam giác GAD.
Cho tứ diện ABCD có \[AB = BC = AC = CD = DB = a,AD = \frac{{a\sqrt 3 }}{2}\]. Gọi M là trung điểm của AB, điểm O là tâm đường tròn ngoại tiếp tam giác BCD. Đường thẳng AO cắt mặt phẳng \[\left( {MCD} \right)\] tại G. Tính diện tích tam giác GAD.


