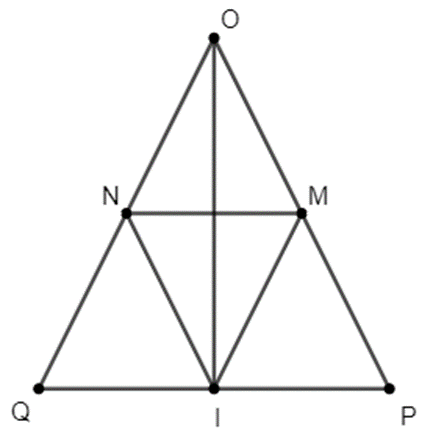
Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ.
(M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
1) Tam giác IMN cân tại I.
2) OI là đường trung trực của MN.
1) Xét ∆OPQ có I là trung điểm của PQ và IN // OP.
Do đó N là trung điểm của OQ (*).
Xét ∆OPQ có I là trung điểm của PQ, IM // OQ.
Do đó M là trung điểm của OP (**).
Từ (*) và (**) suy ra MN là đường trung bình của \(\Delta \)OPQ suy ra MP = NQ.
Xét ∆MPI và ∆NQI có
MP = NQ (cmt)
\(\widehat P = \widehat Q\) (gt)
PI = QI (gt)
Do đó ∆MPI = ∆NQI
Suy ra: IM = IN hay ∆IMN cân tại I.
2) Ta có: OM = ON nên O nằm trên đường trung trực của MN (1)
Ta có: IM = IN nên suy I nằm trên đường trung trực của MN (2)
Từ (1) và (2) suy ra OI là đường trung trực của MN.