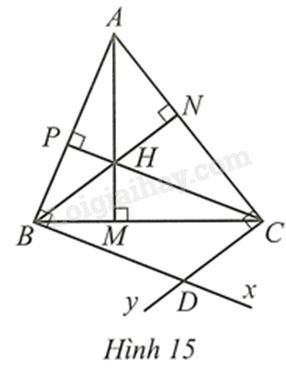
Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB.

Bài 19 trang 95 SBT Toán 8 Tập 1: Cho tam giác nhọn $ABC$ có ba đường cao $AM,BN,CP$ cắt nhau tại $H$. Qua $B$ kẻ tia $Bx$ vuông góc với $AB$. Qua $C$ kẻ tia $Cy$ vuông góc với $AC$. Gọi $D$ là giao điểm của $Bx$ và $Cy$ (Hình 15)

a) Chứng minh tứ giác $BDCH$ là hình bình hành;

b) Tam giác $ABC$ có điều kiện gì thi ba điểm $A,D,H$ thẳng hàng?

c) Tìm mối liên hệ giữa góc $A$ và góc $D$ của tứ giác $ABCD$.

d) Giả sử $H$ là trung điểm của $AM$. Chứng minh diện tích của tam giác $ABC$ bằng diện tích của tứ giác $BHCD$.

Trả lời

a) Ta có: $\widehat{APC}=\widehat{ABD}={90}^{\circ }$ và $\widehat{APC},\widehat{ABD}$ nằm ở vị trí đồng vị nên $CP//BD$.

Tương tự ta chứng minh được $BN//CD$.

Tứ giác $BDCH$ có $BD//CH,BH//CD$ nên $BDCH$ là hình bình hành.

b) Để ba điểm $A,D,H$ thẳng hàng thì $M$ phải thuộc $DH$. Mà $M$ thuộc $BC$, suy ra $M$ là giao điểm của $BC$ và $DH$.

Do $BDCH$ là hình bình hành nên hai đường chéo $BC$ và $DH$ cắt nhau tại trung điểm của mỗi đường. suy ra $M$ là trung điểm $BC$.

Khi đó $\mathrm{\Delta }ABM=\mathrm{\Delta }ACM$ (c.g.c). Suy ra $AB=AC$.

Dễ thấy nếu tam giác $ABC$ có $AB=AC$ thì ba điểm $A,D,H$ thẳng hàng.

Vậy tam giác $ABC$ cân tại $A$ thì $A,D,H$ thẳng hàng.

c)  Xét tứ giác $ABCD$, ta có: $\widehat{BAC}+\widehat{DBA}+\widehat{CDB}+\widehat{ACD}={360}^{\circ }$.

Mà $\widehat{DBA}=\widehat{ACD}={90}^{\circ }$, suy ra tính được $\widehat{BAC}+\widehat{CDB}={3180}^{\circ }$

Vậy góc $A$ và góc $D$của tứ giác $ABCD$ là hai góc bù nhau.

d) Do $H$ là trung điểm của $AM$ nên $HM=\frac{1}{2}AM$

Ta có diện tích tam giác $ABC$ bằng: $\frac{1}{2}.AM.BC=HM.BC$.

Ta chứng minh được $\mathrm{\Delta }BCH=\mathrm{\Delta }CBD$ (c.c.c.). Suy ra diện tích tứ giác $BHCD$ bằng 2 lần diện tích tam giác $BCH$.

Do đó, diện tích tứ giác $BHCD$ bằng: $\left(\frac{1}{2}.HM.BC=HM.BC\right)$ vạy diện tích tam giác $ABC$ bằng điệnt tích của tứ giác $BHCD$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông