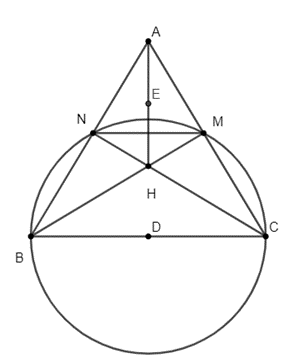
Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB tại N, AC tại M

Đề bài: Cho tam giác nhọn  ABC. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi  H là giao điểm của CN và BM. Khi đó A, N, H, M cùng nằm trên đường tròn nào?

A. (I; IM), I là trung điểm MN;

B. (I; IH), I là trung điểm MN;

C. (F; FA), F là giao điểm đường tròn với AH;

D. (E; EA), E là trung điểm AH.

Trả lời

Hướng dẫn giải:

Đáp án đúng là: D

Ta có: ∆BNC vuông tại N và ∆BMC vuông tại M. (do đường tròn đường kính BC đi qua M, N).

Xét ∆ANH và ∆AMH lần lượt vuông tại N, M.

Với E là trung điểm AH mà AH là cạnh huyền của cả hai tam giác ∆ANH và ∆AMH nên đường tròn tâm (E, EA) sẽ đi qua M, N, H.