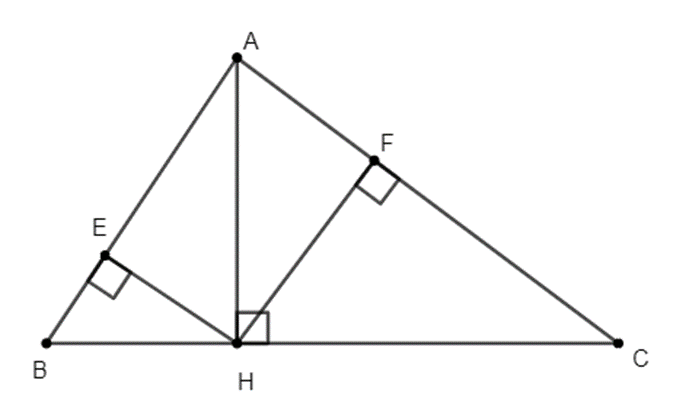
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HE vuông góc với AB và kẻ HF vuông góc với AC.
a) CM: AE.AB = AF.AC;
b) Cho biết AB = 4 cm, AH = 3 cm. Tính AE và BE;
c) Cho biết \[\widehat {HAC} = 30^\circ \]. Tính FC.
a) Áp dụng hệ thức lượng trong tam giác, ta có:
• Xét \(\Delta AHC\): AH2 = AF.AC
• Xét \(\Delta AHB\): AH2 = AE.AB
Do đó AE.AB = AF. AC
b) Ta có: AH2 = AE.AB
\( \Rightarrow AE = \frac{{A{H^2}}}{{AB}} = \frac{{{3^3}}}{4} = 2,25\) (cm)
Mà AE + BE = AB
\( \Rightarrow \)BE = AB – AE
= 4 – 2,24 = 1,75 (cm)
c) \(\Delta AHC\) vuông tại H
\( \Rightarrow \cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
\(AC = \frac{6}{{\sqrt 3 }} = 2\sqrt 3 \) (cm)
Theo ý a) ta có: AE.AB = AF.AC
\( \Rightarrow AF = \frac{{AE.AB}}{{AC}} = \frac{{2,25.4}}{{2\sqrt 3 }} = \frac{{3\sqrt 3 }}{2}\)(cm)
FC = AC – AF
\( = 2\sqrt 3 - \frac{{3\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\)(cm).