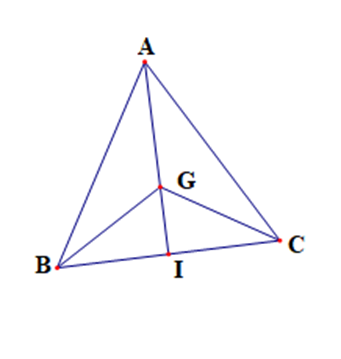
Vì G là trọng tâm tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

Suy ra \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \)

Gọi giao điểm của AG và BC là I

Vì ABC là tam giác đều nên AI ⊥ BC

Hay tam giác ABI vuông tại I

Suy ra AI = \[\sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\]

Do đó AG = \(\frac{2}{3}\)AI = \(\frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)

Vậy \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \frac{{a\sqrt 3 }}{3}\).