Cho tam giác đều cạnh a, trọng tâm G . Tính độ dài vectơ GB + vectơ GC

Đề bài: Cho tam giác đều cạnh a, trọng tâm G . Tính $\left|\overrightarrow{GB}+\overrightarrow{GC}\right|$ .

Trả lời

Hướng dẫn giải:

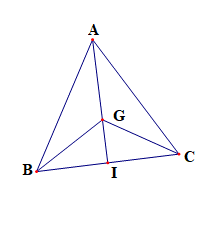
Vì G là trọng tâm tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Suy ra $\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{AG}$

Gọi giao điểm của AG và BC là I

Vì ABC là tam giác đều nên AI ⊥ BC

Hay tam giác ABI vuông tại I

Suy ra AI = $\sqrt{A{B}^2-B{I}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}$

Do đó AG = $\frac{2}{3}$ AI = $\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

Vậy $\left|\overrightarrow{GB}+\overrightarrow{GC}\right|=\frac{a\sqrt{3}}{3}$ .