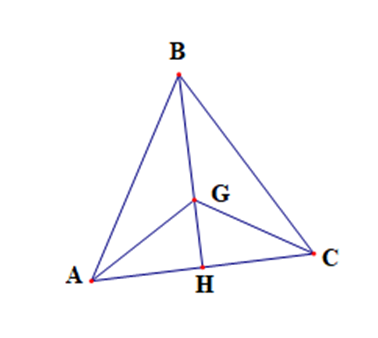
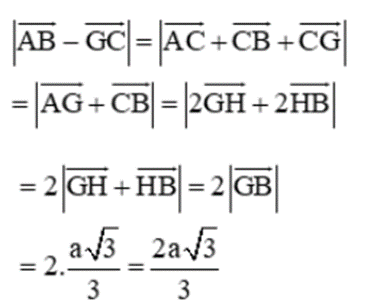Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị vecto AB
Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị \(\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|\) là:
A. \(\frac{a}{3}\);
B. \(\frac{{2a\sqrt 3 }}{3}\);
C. \(\frac{{2a}}{3}\);
D. \(\frac{{a\sqrt 3 }}{3}\).