Cho tam giác ABC. Xác định I sao cho 3 vecto IA - 2 vecto IB + vecto IC
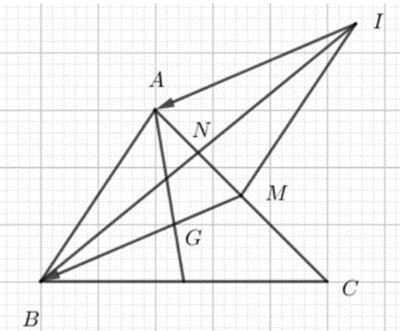
Gọi M là trung điểm của AC
G là trọng tâm tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) và \(\overrightarrow {BG} = \frac{2}{3}\overrightarrow {BM} \)
Ta có \(3\overrightarrow {IA} - 2\overrightarrow {IB} + \overrightarrow {IC} \)
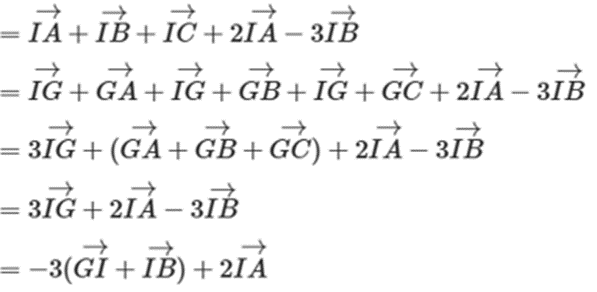
\( = - 3\overrightarrow {GB} + 2\overrightarrow {IA} \)
Mà \(3\overrightarrow {IA} - 2\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)
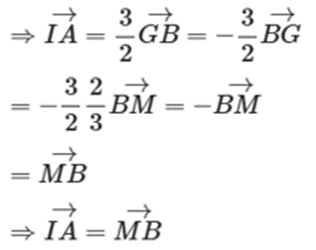
Suy ra I là đỉnh thứ tư của hình bình hành ABMI.
Gọi N là trung điểm của AM, lấy I đối xứng B qua N ta có điểm I thỏa mãn đề bài.