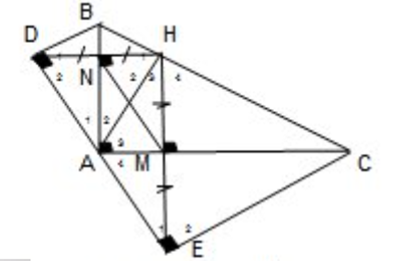
a) Xét tam giác AHE có AM vừa là đường cao vừa là trung tuyến
Do đó tam giác AHE cân tại A
Suy ra AH = AE, AH là tia phân giác của \(\widehat {HA{\rm{E}}}\)
Suy ra \(\widehat {HAM} = \widehat {MAE} = \frac{1}{2}\widehat {HA{\rm{E}}}\)
Xét tam giác AHD có AN vừa là đường cao vừa là trung tuyến
Do đó tam giác AHD cân tại A
Suy ra AH = AD, AN là tia phân giác của \(\widehat {HA{\rm{D}}}\)
Suy ra \(\widehat {HAN} = \widehat {NAD} = \frac{1}{2}\widehat {HAD}\)
Ta có:
\(\widehat {DA{\rm{E}}} = \widehat {DAN} + \widehat {NAH} + \widehat {HAM} + \widehat {MA{\rm{E}}} = 2\widehat {NAH} + 2\widehat {HAM} = 2\widehat {BAC} = 2.90^\circ = 180^\circ \)
Suy ra D, A, E thẳng hàng
b) Xét tam giác EDH có M là trung điểm của EH, N là trung điểm của DH
Suy ra MN là đường trung bình
Do đó MN // DE
c) Xét △AHB và △ADB có
AB là cạnh chung
\(\widehat {HAB} = \widehat {BAD}\)(chứng minh câu a)
AH = AD (chứng minh câu a)
Do đó △AHB = △ADB (c.g.c)
Suy ra \(\widehat {AHB} = \widehat {ADB}\) (hai góc tương ứng)
Mà \(\widehat {AHB} = 90^\circ \) nên \(\widehat {ADB} = 90^\circ \)
Hay AD ⊥ BD (1)
Xét △AHC và △AEC có
AC là cạnh chung
\(\widehat {HAC} = \widehat {EAC}\)(chứng minh câu a)
AH = AE (chứng minh câu a)
Do đó △AHC = △AEC (c.g.c)
Suy ra \(\widehat {AHC} = \widehat {AEC}\) (hai góc tương ứng)
Mà \(\widehat {AHC} = 90^\circ \) nên \(\widehat {AEC} = 90^\circ \)
Hay AE ⊥ EC (2)
Từ (1) và (2) suy ra EC // BD
d) Ta có AD = AH, AE = AH (chứng minh câu a)
Suy ra AD = AE = AH
Xét tứ giác AMHN có
\(\widehat {ANH} = \widehat {AMH} = \widehat {MAN} = 90^\circ \)
Suy ra AMHN là hình chữ nhật
Do đó \(\widehat {MHN} = 90^\circ \)
Hay tam giác DEH vuông tại H
Vậy AD = AE = AH và DHE vuông tại H.