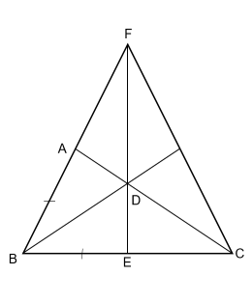
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng.

Xét ΔABD và ΔEBD có:

AB = BE (gt);

$\widehat{ABD}=\widehat{EBD}$(BD là tia phân giác $\widehat{ABC}$ )

BD cạnh chung

⇒∆ABD = ∆EBD (c.g.c)

$\Rightarrow \widehat{BAD}=\widehat{BED}$

Mà $\widehat{BAD}=90°$ (gt)

$\Rightarrow \widehat{BED}=90°$

Suy ra: DE vuông BC

Mặc khác ∆FBC có CA, BD là đường cao cắt nhau tại D.

⇒ D là trực tâm của ∆FBC có DF ⊥ BC.

Ta có DE ⊥ BC; DF ⊥ BC.

Do đó hai đường thẳng DE, DF trùng nhau.

Vậy ba điểm D, E, F thẳng hàng.