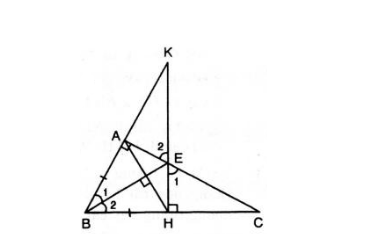
Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc BC (H thuộc BC).
37
04/05/2024
Cho ABC vuông tại A; đường phân giác BE. Kẻ EH BC (H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) ΔABE = ΔHBE.
b) BE là đường trung trực của đoạn thẳng AH.
c) EK = EC.
d) AE < EC.
Trả lời
a) Xét và ta có :
BE là cạnh chung
Do đó (cạnh huyền – góc nhọn).
b) Vì (chứng minh trên)
Suy ra BA = BH, EA = EH (các cặp cạnh tương ứng)
EB là đường trung trực của AH.
c) Xét và ta có:
AE = EH (chứng minh trên)
(hai góc đối đỉnh).
Do đó (g.c.g).
Suy ra EK = EC (hai cạnh tương ứng).
d) vuông tại H có EH < EC (do cạnh huyền là lớn nhất trong tam giác vuông).
Mà EH = AE (câu b) nên AE < EC.