Cho tam giác ABC vuông tại A, đường cao AM. Gọi H, K lần lượt là hình chiếu của M trên AB, AC. Biết AM = 4

Câu 40: Cho tam giác ABC vuông tại A, đường cao AM. Gọi H, K lần lượt là hình chiếu của M trên AB, AC. Biết AM = 4 cm. Tính HA.HB + KA.KC.

Trả lời

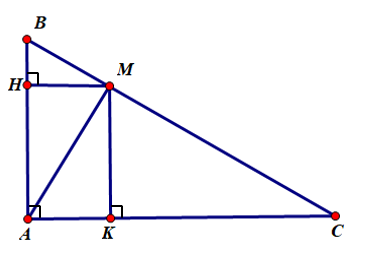
Xét ΔAMB vuông tại M có MH là đường cao nên:

HA.HB = HM²     (1)  (hệ thức lượng trong tam giác vuông)

Xét ΔAMC vuông tại M có MK là đường cao nên:

KA.KC = KM²    (2) (hệ thức lượng trong tam giác vuông)

Tứ giác AHMK có:

$\widehat{AHM}=\widehat{MKA}=\widehat{HAK}=90°$

Suy ra AHMK là hình chữ nhật

Do đó AH = KM

Từ (1) và (2) ta có:

HA.HB + KA.KC = HM² + KM²

HA.HB + KA.KC = HM² + AH²

HA.HB + KA.KC = AM² (áp dụng định lý Pythagore cho tam giác vuông AHM)

HA.HB + KA.KC = 4² = 16

Vậy HA.HB + KA.KC = 16.