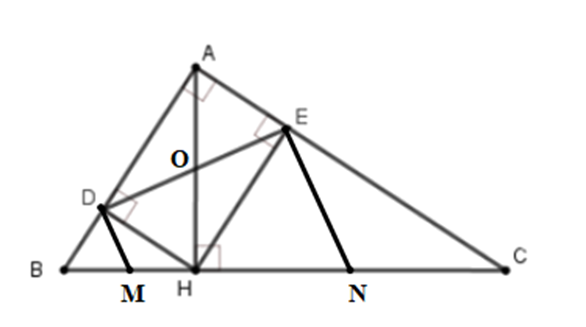
a) Xét tứ giác ADHE có AD // EH và DH // AE
Suy ra ADHE là hình bình hành
Mà \(\widehat {DA{\rm{E}}} = 90^\circ \)
Suy ra ADHF là hình chữ nhật.
b) Áp dụng định lý Pytago trong tam giác vuông ABC có:
BC2 = AB2 + AC2
Thay số: BC2 = 62 + 82 = 100
Suy ra BC = 10
Xét tam giác ABC vuông tại A có AH . BC = AB . AC
Thay số: AH . 10 = 6 . 8
Suy ra AH = 4,8
Vì tam giác ABH vuông tại H, theo định lý Pytago ta có
AB2 = AH2 + HB2
Thay số: 62 = 4,82 + HB2
Suy ra BH = 3,6
Vì tam giác BHD vuông tại D có DM là trung tuyến
Suy ra \[DM = MH = \frac{1}{2}BH = \frac{1}{2}.3,6 = 1,8\]
Ta có CH = BC – BH = 10 – 4,8 = 5,2.
Vì tam giác CHE vuông tại E có EN là trung tuyến
Suy ra \[EN = NH = \frac{1}{2}CH = \frac{1}{2}.5,2 = 2,6\].
Ta có DM + EN = 1,8 + 2,6 = 4,4 (cm)
c) Gọi O là giao điểm của AH và DE.
Vì ADHE là hình chữ nhật nên O là trung điểm của AH, DE và AH = DE.
Suy ra OA = OD = OE = OH
Do đó tam giác OHD cân tại O
Suy ra \(\widehat {O{\rm{D}}H} = \widehat {OH{\rm{D}}}\)
Vì DM = MH (chứng minh câu b) nên tam giác DMH cân tại M
Suy ra \(\widehat {{\rm{MD}}H} = \widehat {MH{\rm{D}}}\)
Ta có \(\widehat {MHD} + \widehat {OH{\rm{D}}} = \widehat {AHB} = 90^\circ \)
Mà \(\widehat {O{\rm{D}}H} = \widehat {OH{\rm{D}}}\), \(\widehat {{\rm{MD}}H} = \widehat {MH{\rm{D}}}\)
Suy ra \(\widehat {MDH} + \widehat {O{\rm{DH}}} = \widehat {M{\rm{D}}O} = 90^\circ \)
Do đó DM ⊥ DO (1)
Vì OE = OH
Do đó tam giác OEH cân tại O
Suy ra \(\widehat {OEH} = \widehat {OHE}\)
Vì HN = EN (chứng minh câu b) nên tam giác ENH cân tại N
Suy ra \(\widehat {{\rm{NE}}H} = \widehat {NHE}\)
Ta có \(\widehat {OHE} + \widehat {EHN} = \widehat {AHN} = 90^\circ \)
Mà \(\widehat {OEH} = \widehat {OHE}\), \(\widehat {{\rm{NE}}H} = \widehat {NHE}\)
Suy ra \(\widehat {OEH} + \widehat {OEN} = \widehat {OEN} = 90^\circ \)
Do đó EN ⊥ EO (2)
Từ (1) và (2) suy ra DM // EN
Vậy DENM là hình thang.