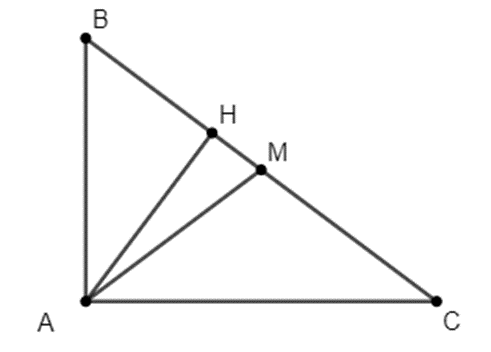
Vì \(\Delta \)ABC vuông tại A và AH là đường cao nên ta có:

AH² = BH.HC \( \Leftrightarrow \)AH² = 4.9 = 36 \( \Leftrightarrow \) AH = 6 (cm).

Vì AM là đường trung tuyến của ∆ABC nên ta có:
\(AM = \frac{1}{2}BC = \frac{1}{2}\left( {4 + 9} \right) = \frac{{13}}{2}\)

\( \Rightarrow HM = \sqrt {A{M^2} - A{H^2}} = \sqrt {{{\left( {\frac{{13}}{2}} \right)}^2} - {6^2}} = \frac{5}{2}\)

\( \Rightarrow {S_{AHM}} = \frac{1}{2}AH.HM = \frac{1}{2}.6.\frac{5}{2} = \frac{{15}}{2}\) (cm²)