Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh BE2 + CF2 ≥ EF2, khi nào dấu “=” xảy ra?
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh BE2 + CF2 ≥ EF2, khi nào dấu “=” xảy ra?
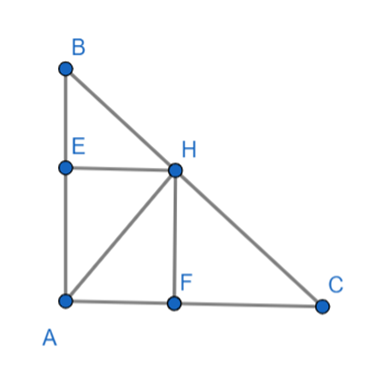
Xét tam giác CFH và tam giác CAB có:
\(\widehat C\) chung
\(\widehat {CFH} = \widehat {CAB}\)(bằng 90 độ)
Suy ra: ∆CFH ᔕ ∆CAB (g.g)
Nên: \[\frac{{CF}}{{CA}} = \frac{{CH}}{{CB}}\,\,hay\,\,\frac{{CF}}{{CH}} = \frac{{CA}}{{CB}}\, \Rightarrow \,C{F^2} = \frac{{C{A^2}\,.\,C{H^2}\,}}{{C{B^2}}} = \frac{{C{H^3}\,}}{{CB}}\]( vì CA = CH.CB) (1)
Tương tự: ∆BEH ᔕ ∆BAC (g.g)
Suy ra: \[\frac{{BE}}{{BH}} = \frac{{BA}}{{BC}}\,\, \Rightarrow \,B{E^2} = \frac{{B{A^2}\,.\,B{H^2}\,}}{{B{C^2}}} = \frac{{B{H^3}}}{{BC}}\](vì BA2 = BH. BC) (2)
TỪ (1) và (2) ta có:
\[\sqrt[3]{{B{E^2}}} + {\rm{ }}\sqrt[3]{{C{F^2}}} = \,\frac{{BH + CH}}{{\sqrt[3]{{BC}}}} = \sqrt[3]{{B{C^2}}}\]
Áp dụng bất đẳng thức: a3 + b3 ≥ \[\frac{{{{\left( {a + b} \right)}^3}}}{4}\] ta có:
BE2 + CF2 ≥ \[\frac{{{{\left( {\sqrt[3]{{B{E^2}}} + \sqrt[3]{{C{F^2}}}} \right)}^2}}}{4} = \frac{{B{C^2}}}{4}\]
MÀ AH ≤ \(\frac{1}{2}BC\)(vì AH luôn nhỏ hơn đường trung tuyến kẻ từ A xuống BC)
Suy ra: AH2 ≤ \(\frac{1}{4}B{C^2}\)
Mặt khác: AHEF là hình chữ nhật (vì có 3 góc vuông) nên AH = EF
Vậy: BE2 + CF2 ≥ EF2
Dấu “=” khi tam giác ABC vuông cân tại A.