Lời giải
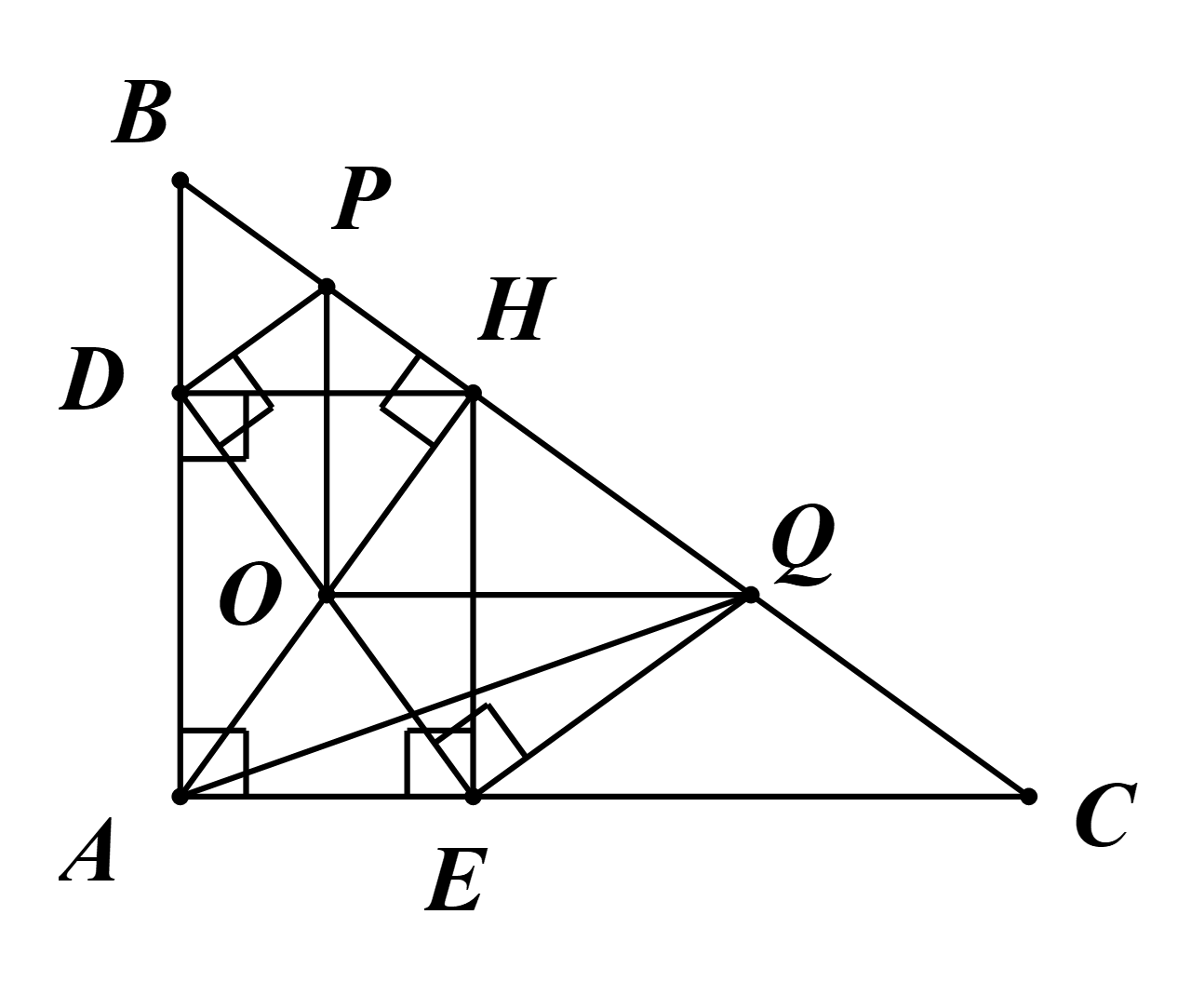
a) Ta có \(\widehat {HEA} = \widehat {EAD} = \widehat {ADH} = 90^\circ \).
Suy ra tứ giác ADHE là hình chữ nhật.
Do đó DE = AH.
b) Ta có O là giao điểm của DE và AH.
Suy ra OE = OH = OA = OD.
Tam giác BDH vuông tại D có DP là đường trung tuyến.
Suy ra DP = PH.
Xét ∆PDO và ∆PHO, có:
PO là cạnh chung;
DP = PH (chứng minh trên);
DO = OH (chứng minh trên).
Do đó ∆ PDO = ∆ PHO (c.c.c).
Suy ra \(\widehat {PDO} = \widehat {PHO} = 90^\circ \) (cặp góc tương ứng).
Vì vậy DP ⊥ DE (1)
Chứng minh tương tự, ta được QE ⊥ DE (2)
Từ (1), (2), suy ra DP // QE.
Ta có DP // QE (chứng minh trên) và \(\widehat {PDE} = \widehat {DEQ} = 90^\circ \) (chứng minh trên).
Vậy tứ giác DEQP là hình thang vuông.
c) Tam giác AHC có O, Q lần lượt là trung điểm của AH và HC.
Suy ra OQ là đường trung bình của tam giác AHC.
Do đó OQ // AC.
Mà AC ⊥ AB (tam giác ABC vuông tại A).
Vì vậy OQ ⊥ AB.
Tam giác ABQ có AH, QO là hai đường cao cắt nhau tại O.
Vậy O là trực tâm của tam giác ABQ.
d) Ta có \({S_{DEQP}} = \frac{1}{2}DE\left( {DP + QE} \right) = \frac{1}{2}AH\left( {\frac{1}{2}BH + \frac{1}{2}CH} \right)\)
\( = \frac{1}{4}AH\left( {BH + CH} \right) = \frac{1}{4}AH.BC = \frac{1}{2}{S_{ABC}}\).
Vậy SABC = 2SDEQP.

