Cho tam giác ABC vuông tại A đường cao AH, I là trung điểm của AB. Lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D a) AKHD là hình gì? b) Chứng minh tứ giác A
26
18/05/2024
Cho tam giác ABC vuông tại A đường cao AH, I là trung điểm của AB. Lấy K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D
a) AKHD là hình gì?
b) Chứng minh tứ giác AHBD là hình chữ nhật
c) Tam giác ABC phải có thêm điều kiện gì để AHBD là hình vuông
d) M là điểm đối xứng với A qua H. Chứng minh AK vuông góc với CM.
Trả lời
Lời giải
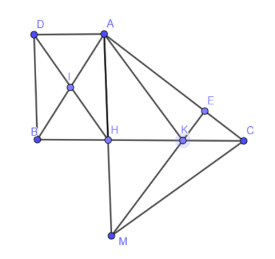
a) Xét tam giác ABK có I là trung điểm của AB, H là trung điểm của BK
Do đó HI là đường trung bình
Suy ra HI // AK
Xét tứ giác AKHD có HI // AK, AD // HK
Suy ra AKHD là hình bình hành
Vậy AKHD là hình bình hành
b) Vì AKHD là hình bình hành (chứng minh câu a)
Nên AD = HK
Mà BH = HK (giả thiết)
Suy ra AD = BH
Vì AH ⊥ BC nên \(\widehat {AHB} = 90^\circ \)
Xét tứ giác AHBD có AD = BH, AD // BH (chứng minh trên)
Suy ra AHBD là hình bình hành
Mà \(\widehat {AHB} = 90^\circ \)
Suy ra AHBD là hình chữ nhật
Vậy AHBD là hình chữ nhật
c) Để hình chữ nhật AHBD là hình vuông thì AH = BH
⟺ Tam giác ABK vuông tại A (vì AH = BH = HK)
⟺ K ≡ C (vì tam giác ABC vuông tại A)
⟺ H là trung điểm của BC
⟺ tam giác ABC cân tại A
Vậy tam giác ABC vuông cân thì AHBD là hình vuông
d) Xét tứ giác ABMK có hai đường chéo AM và BK cắt nhau tại trung điểm H của mỗi đường
Suy ra ABMK là hình bình hành
Suy ra AB // MK
Mà AB ⊥ AC
Do đó MK ⊥ AC
Xét tam giác AMC có MK, CH là hai đường cao
MK cắt CH tại K
Suy ra K là trực tâm tam giác AMC
Do đó AK ⊥ MC
Vậy AK ⊥ MC.
