Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:

a) EF = AH.

b) AM ⊥ EF.

Lời giải

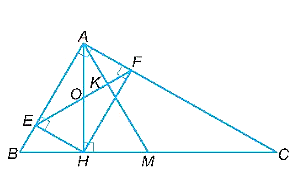
a)Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \).

Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.

Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).

Xét tứ giác AFHE có: \(\widehat {BAC} = \widehat {HEA} = \widehat {HFA} = 90^\circ \).

Do đó, tứ giác AFHE là hình chữ nhật.

Suy ra AH = FE (hai đường chéo bằng nhau).

b) Vì tứ giác AFHE là hình chữ nhật nên \(\widehat {FHE} = 90^\circ \).

Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên

AM = MB = MC = \(\frac{1}{2}BC\).

Tam giác AMB có AM = MB nên tam giác AMB cân tại M.

Do đó, \(\widehat {MAB} = \widehat B\).

Lại có \(\widehat B = \widehat {AHE}\,\,\,\,\,\left( { = 90^\circ - \widehat {HEB}} \right)\).

Nên \(\widehat {MAB} = \widehat {AHE}\) (1).

Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.

Do đó, OH = OE = OF = OA.

Tam giác OAE có OA = OE nên tam giác OAE cân tại O.

Suy ra \(\widehat {OEA} = \widehat {OAE}\).

Mà AE song song với FH (do AFHE là hình chữ nhật) nên \(\widehat {OHF} = \widehat {OAE}\) (hai góc so le trong).

Do đó, \(\widehat {OEA} = \widehat {OHF}\) (2).

Lại có \(\widehat {OHF} + \widehat {OHE} = \widehat {FHE} = 90^\circ \) (3).

Từ (1), (2), (3) ta có: \[\widehat {MAB} + \widehat {OEA} = 90^\circ \].

Gọi K là giao điểm của AM và EF. Khi đó, \[\widehat {KAE} + \widehat {KEA} = 90^\circ \]. Suy ra \(\widehat {AKE} = 90^\circ \).

Vậy AM vuông góc với EF tại K.