Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Lấy điểm D trên cạnh BC sao cho BD = 2 cm. Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.

a) Chứng minh rằng ∆BDE ᔕ ∆DCF.

b) Tính độ dài đoạn thẳng AD.

Lời giải

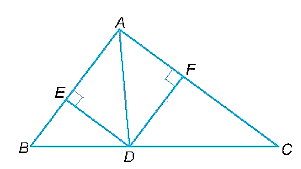
a) Xét tam giác ABC có:

AB² + AC² = BC² (do 3² + 4² = 5²).

Nên tam giác ABC vuông tại A (định lí Pythagore đảo).

Ta có DE, DF lần lượt vuông góc với AB, AC tại E và F.

Do đó, $\widehat {DFC} = \widehat {DFA} = \widehat {DEA} = \widehat {DEB} = 90^\circ$.

Xét tứ giác AEDF có: $\widehat {DFA} = \widehat {DEA} = \widehat {FAE} = 90^\circ$.

Nên tứ giác AEDF là hình chữ nhật.

Do đó, $\widehat {FDE} = 90^\circ$.

Mà $\widehat {CDF} + \widehat {FDE} + \widehat {EDB} = 180^\circ$. Suy ra $\widehat {CDF} + \widehat {EDB} = 90^\circ$.

Xét tam giác BDE và tam giác DCF có:

$\widehat {DEB} = \widehat {DFC} = 90^\circ$

$\widehat B = \widehat {FDC}$ $\left( { = 90^\circ - \widehat {EDB}} \right)$

Do đó, ∆BDE ᔕ ∆DCF (g.g).

b) Tam giác ABC có: DE // AC (cùng vuông góc với AB).

Nên ∆BDE ᔕ ∆BCA.

Do đó, $\frac{{ED}}{{AC}} = \frac{{EB}}{{AB}} = \frac{{BD}}{{BC}}$.

Suy ra $\frac{{DE}}{4} = \frac{{EB}}{3} = \frac{2}{5}$.

Do đó, DE = $\frac{8}{5}$cm, EB = $\frac{6}{5}$cm.

Suy ra AE = AB – EB = 3 – $\frac{6}{5}$ = $\frac{9}{5}$ cm.

Áp dụng định lí Pythagore vào tam giác AED vuông tại E có:

AD² = AE² + ED² = ${\left( {\frac{9}{5}} \right)^2} + {\left( {\frac{8}{5}} \right)^2} = \frac{{29}}{5}$.

Suy ra $AD = \sqrt {\frac{{29}}{5}}$cm.