Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:

a) AE . AB = AF . AC.

b) ∆ADE ᔕ ∆AHC và ∆ANF ᔕ ∆AMB.

Lời giải

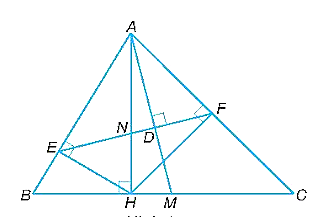
a) Vì AH là đường cao của tam giác ABC nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \).

Vì HE, HF vuông góc với AB, AC nên ta có:

\(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = 90^\circ \).

Tam giác HEA và tam giác BHA có:

\(\widehat {HEA} = \widehat {AHB} = 90^\circ \)

\(\widehat {BAH}\) chung

Do đó, ∆HEA ᔕ ∆BHA (g.g).

Suy ra \(\frac{{AE}}{{AH}} = \frac{{AH}}{{AB}}\) nên AE . AB = AH² (1).

Tam giác HFA và tam giác CHA có:

\(\widehat {HFA} = \widehat {AHC} = 90^\circ \)

\(\widehat {CAH}\) chung

Do đó, ∆HFA ᔕ ∆CHA (g.g).

Suy ra \(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}}\) nên AF . AC = AH² (2).

Từ (1) và (2) suy ra AE . AB = AF . AC.

b) Vì AE . AB = AF . AC nên \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).

Tam giác AEF và tam giác ACB có:

\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\)

\(\widehat {BAC}\) chung

Do đó, ∆AEF ᔕ ∆ACB (c.g.c).

Suy ra \(\widehat {AEF} = \widehat C\).

Tam giác AED và tam giác ACH có:

\(\widehat {ADE} = \widehat {AHC} = 90^\circ \)

\(\widehat {AEF} = \widehat C\) (cmt)

Do đó, ∆ADE ᔕ ∆AHC (g.g).

Suy ra \(\widehat {EAD} = \widehat {CAH}\).

Do đó, \(\widehat {NAF} = \widehat {CAH} = \widehat {EAD} = \widehat {MAB}\).

Hai tam giác ANF và AMB có:

\(\widehat {NAF} = \widehat {MAB}\) (chứng minh trên)

\(\widehat {AFN} = \widehat {AFE} = \widehat {ABC} = \widehat {ABM}\) (do ∆AEF ᔕ ∆ACB)

Do đó ∆ANF ᔕ ∆AMB (g.g).