Lời giải
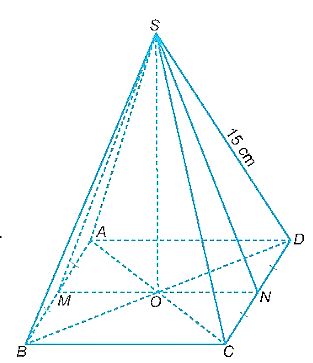
a) Vì các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau nên các đường trung tuyến tương ứng của chúng bằng nhau, tức là SM = SN.
Do đó, tam giác SMN là tam giác cân tại S và O là trung điểm của MN nên SO ⊥ MN.
(Vì M và N lần lượt là trung điểm của AB và CD trong hình vuông ABCD với O là giao điểm của hai đường chéo nên ta chứng minh được O là trung điểm của MN).
Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore ta có:
AC2 = AB2 + BC2 = 102 + 102 = 200 nên AC = \(10\sqrt 2 \) cm.
Do đó, BD = AC = \(10\sqrt 2 \) cm, suy ra DO = \(\frac{1}{2}\)BD = \(5\sqrt 2 \) cm.
Xét tam giác SOD vuông tại O, áp dụng định lý Pythagore ta có:
DO2 + SO2 = SD2
Suy ra SO2 = SD2 – DO2 = 152 – \({\left( {5\sqrt 2 } \right)^2}\) = 175.
Nên SO = \(\sqrt {175} = 5\sqrt 7 \) cm.
b) Thể tích của hình chóp tứ giác đều S.ABCD là:
\({V_{S.ABCD}} = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot 5\sqrt 7 \cdot {10^2} = \frac{{500\sqrt 7 }}{3}\) (cm3).
c) Ta có SM là trung tuyến trong tam giác cân SAB nên SM đồng thời là đường cao.
Do đó, SM là một trung đoạn của hình chóp tứ giác đều.
Ta có SA = SD = 15 cm, AM = \(\frac{1}{2}\)AB = 5 cm.
Xét tam giác SMA vuông tại M, áp dụng định lý Pythagore ta có:
SM2 + AM2 = SA2
Do đó, SM2 = SA2 – AM2 = 152 – 52 = 200 nên SM = \(10\sqrt 2 \) cm.
Nửa chu vi đáy ABCD là: p = 10 . 4 : 2 = 20 cm.
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = SM \cdot p = 10\sqrt 2 \cdot 20 = 200\sqrt 2 \) (cm2).
Diện tích đáy ABCD là: SABCD = 102 = 100 (cm2).
Diện tích toàn phần của hình chóp S.ABCD là:
\({S_{tp}} = {S_{xq}} + {S_{ABCD}} = 200\sqrt 2 + 100 = 100\left( {2\sqrt 2 + 1} \right)\) (cm2).

