Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho \(\frac{{MB}}{{MA}} = \frac{1}{3}\), N là điểm trên cạnh BC sao cho \(\frac{{NB}}{{NC}} = \frac{1}{3}\).

a) Chứng minh MN // AC và MN = \(\frac{1}{4}\)AC.

b) Gọi K là giao điểm của AN và CM. Chứng minh \[\frac{{KN}}{{KA}} = \frac{{KM}}{{KC}} = \frac{1}{4}\].

c) Nếu thay điều kiện \(\frac{{MB}}{{MA}} = \frac{1}{3}\) và \(\frac{{NB}}{{NC}} = \frac{1}{3}\) bằng điều kiện CM là phân giác của góc C, AN là phân giác của góc A thì tam giác ABC phải thỏa mãn điều kiện gì để MN // AC?

Lời giải

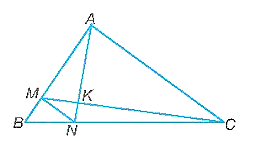
a) Xét tam giác ABC có:

\(\frac{{MB}}{{MA}} = \frac{{NB}}{{NC}}\,\,\,\,\left( { = \frac{1}{3}} \right)\)

Nên MN // AC (định lí Thalès đảo).

Vì \(\frac{{MB}}{{MA}} = \frac{1}{3}\) nên MA = 3MB.

Tam giác ABC có MN // AC nên \[\frac{{MN}}{{AC}} = \frac{{BM}}{{AB}} = \frac{{BM}}{{BM + MA}} = \frac{{BM}}{{4BM}} = \frac{1}{4}\].

Suy ra MN = \(\frac{1}{4}\)AC.

b) Tam giác MNK có MN // AC nên \(\frac{{KN}}{{KA}} = \frac{{KM}}{{KC}} = \frac{{MN}}{{AC}} = \frac{1}{4}\).

c) Nếu MN // AC thì \(\frac{{MB}}{{MA}} = \frac{{NB}}{{NC}}\) (định lí Thalès) (1).

Vì CM là tia phân giác của góc BCA trong tam giác ABC nên \(\frac{{MB}}{{MA}} = \frac{{BC}}{{AC}}\) (2).

Vì AN là tia phân giác của góc BAC trong tam giác ABC nên \(\frac{{NB}}{{NC}} = \frac{{AB}}{{AC}}\) (3).

Từ (1), (2), (3) suy ra \(\frac{{AB}}{{AC}} = \frac{{BC}}{{AC}}\) nên AB = BC.

Do đó, tam giác ABC cân tại B.

Ngược lại, nếu tam giác ABC cân tại B, CM là phân giác của góc C, AN là phân giác góc A thì dễ thấy MN // AC.

Vậy để MN // AC thì điều kiện là tam giác ABC cân tại B.