Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là 54 cm^2 và 96 cm^2. Tính AB, AC, BC.

Trả lời

Lời giải

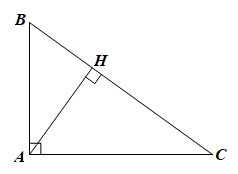
Ta có: \({S_{ABH}} = \frac{1}{2}AH.BH = 54 \Rightarrow AH.BH = 108\)

           \({S_{ACH}} = \frac{1}{2}AH.CH = 96 \Rightarrow AH.CH = 192\)

Þ AH.BH.AH.CH = 108.192 = 20 736

Þ AH².BH.CH = 20 736 (*)

Xét tam giác ABC vuông tại A có đường cao AH, theo hệ thức lượng ta có:

AH² = BH.CH

Thay vào (*) ta được: AH².AH² = 20 736

Þ AH⁴ = 20 736 = 12⁴

Þ AH = 12 cm.

\( \Rightarrow BH = \frac{{108}}{{12}} = 9\left( {cm} \right)\) và \(CH = \frac{{192}}{{12}} = 16\left( {cm} \right)\)

• Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

AB² = AH² + BH² = 12² + 9² = 225 Þ AB = 15 (cm).

• Xét tam giác ACH vuông tại H, theo định lí Pytago ta có:

AC² = AH² + CH² = 12² + 16² = 400 Þ AC = 20 (cm).

• BC = BH + CH = 9 + 16 = 25 (cm).