Cho tam giác ABC vuông tại A, đường cao AH.

a) Chứng minh AB² = BH.BC.

b) Chứng minh AC² = CH.BC.

c) Chứng minh \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).

Lời giải

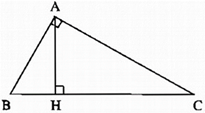
a) Xét ∆HAB và ∆ACB có:

\(\widehat {AHB} = \widehat {CAB}\left( { = {{90}^ \circ }} \right)\)

\(\widehat B\) chung

Do đó ∆HAB ᔕ ∆ACB (g.g)

Suy ra \(\frac{{HB}}{{AB}} = \frac{{AB}}{{CB}}\) (các cặp cạnh tương ứng tỉ lệ).

Vậy \(A{B^2} = BH\,.\,BC\) (đpcm)

b) Xét ∆HAC và ∆ABC có:

\(\widehat {AHC} = \widehat {BAC}\left( { = {{90}^ \circ }} \right)\)

\(\widehat C\): góc chung

Þ ∆HAC ᔕ ∆ABC (g.g)

\( \Rightarrow \frac{{HC}}{{AC}} = \frac{{AC}}{{BC}} \Rightarrow A{C^2} = CH\,.\,CB\) (đpcm)

c) Ta có: \(\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BH\,.\,BC}} + \frac{1}{{CH\,.\,CB}}\)

\( = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right) = \frac{1}{{BC}}.\frac{{CH + BH}}{{BH\,.\,CH}}\)

\( = \frac{1}{{BC}}.\frac{{BC}}{{BH\,.\,CH}} = \frac{1}{{BH\,.\,CH}}\) (1)

Lại có \(\widehat {HAB} = \widehat {HCA}\) (hai góc phụ \(\widehat {HAC}\))

Xét ∆HAB và ∆HCA có:

\(\widehat {HAB} = \widehat {HCA}\) (cmt)

\(\widehat {AHB} = \widehat {CHA}\;\left( { = {{90}^ \circ }} \right)\)

Þ ∆HAB ᔕ ∆HCA (g.g)

\( \Rightarrow \frac{{HA}}{{HC}} = \frac{{HB}}{{HA}} \Rightarrow A{H^2} = CH\,.\,BH\) (2)