Lời giải
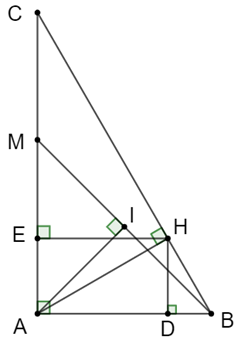
a) ∆ABC vuông tại A
\( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{4^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 8\;(cm)\)
\(\sin \widehat {ACB} = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2} \Rightarrow \widehat {ACB} = 30^\circ \)
\( \Rightarrow \widehat {ABC} = 180^\circ - \widehat {BAC} - \widehat {ACB} = 180^\circ - 90^\circ - 30^\circ = 60^\circ \)
b) Tứ giác ADHE có \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên tứ giác ADHE là hình chữ nhật
Þ DE = AH và \(\widehat {DHE} = 90^\circ \)
Þ ∆DHE vuông tại H Þ DH2 + EH2 = DE2
Xét ∆ADH và ∆HDB có:
\(\widehat {ADH} = \widehat {HDB}\;\left( { = {{90}^ \circ }} \right)\)
\(\widehat {DAH} = \widehat {DHB}\) (cùng phụ \(\widehat {AHD}\))
Do đó ∆ADH ᔕ ∆HDB (g.g)
\( \Rightarrow \frac{{EA}}{{EH}} = \frac{{EH}}{{CE}} \Rightarrow EA.EC = E{H^2}\)
Þ BD.DA + CE.EA = DH2 + EH2 = DE2 = AH2.
Vậy BD.DA + CE.EA = AH2 (đpcm).
c) Ta có \(\widehat {AIB} = \widehat {AHB} = 90^\circ \) nên I, H thuộc đường tròn đường kính AB
Þ Tứ giác ABHI nội tiếp đường tròn đường kính AB
\( \Rightarrow \widehat {BAH} = \widehat {BIH}\) (góc nội tiếp chắn cung BM)
Mà \(\widehat {BAH} = \widehat {BCM}\) (cùng phụ \(\widehat {CAM}\))
Nên \(\widehat {BIH} = \widehat {BCM}\)
• Xét ∆BIH và ∆BCM có:
\(\widehat B\) chung
\(\widehat {BIH} = \widehat {BCM}\) (cmt)
Do đó ∆BIH ᔕ ∆BCM (g.g)
Suy ra \(\frac{{BH}}{{BM}} = \frac{{HI}}{{CM}}\) (các cạnh tương ứng tỉ lệ)
• Xét ∆BAM và ∆BCA có:
\(\widehat B\) chung
\(\widehat {BMA} = \widehat {BAC}\;\left( { = {{90}^ \circ }} \right)\) (cmt)
Do đó ∆BAM ᔕ ∆BCA (g.g)
\( \Rightarrow \frac{{BH}}{{BA}} = \frac{{AB}}{{BC}} \Rightarrow BH = \frac{{A{B^2}}}{{BC}} \Rightarrow \frac{{A{B^2}}}{{BC.BM}} = \frac{{HI}}{{CM}}\)
Khi đó \(\sin \widehat {AMB}\,\,.\,\,\sin \widehat {ACB} = \frac{{AB}}{{BM}}\,.\,\frac{{AB}}{{BC}} = \frac{{A{B^2}}}{{BM\,.\,BC}} = \frac{{HI}}{{CM}}\).
Vậy \[\sin \widehat {AMB}\,.\,\sin \widehat {ACB} = \frac{{HI}}{{CM}}\] (đpcm).

